Упражнение 129 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 49
Вернуться к содержанию учебника
Вопрос
Площадь круга \(S\) (см\(^2\)) вычисляется по формуле \( S = \pi r^{2}, \) где \(r\) (см) — радиус круга. Постройте график функции \(S = \pi r^{2} \) и найдите по графику:
а) площадь круга, если его радиус равен 1,3 см; 0,8 см; 2,1 см;
б) радиус круга, площадь которого равна 1,8 см\(^2\); 2,5 см\(^2\); 6,5 см\(^2\).
Подсказка
Вспомните:
- График функции.
- Квадратичную функцию и ее график.
- Положение точек на координатной плоскости.
- Степень с натуральным показателем.
- Умножение десятичных чисел.
- Чему равно число \(\pi\).
Ответ
\( S = \pi r^{2}, \pi=3,14. \)
| \(r\) | 0 | 1 | 1,5 | 2 | 2,5 |
| \(S\) | 0 | 3,14 | 7,1 | 12,6 | 19,6 |
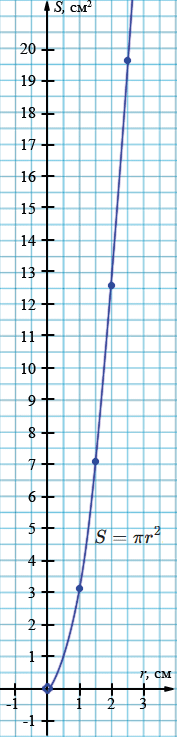
а) При \( r = 1,3\) \( S =5,3\) см2.
При \( r = 0,8\) \(S =2 \) см2.
При \( r = 2,1\) \(S =3,8\) см2.
б) \( S = 1,8\) при \(r = 0,7\) см.
\( S = 2,5\) при \(r = 0,9\) см.
\( S = 6,5\) при \(r =1,4\) см.
Пояснения:
1. Формула площади круга:
\[ S = \pi r^{2}. \]
Это квадратичная зависимость: чем больше радиус, тем быстрее увеличивается площадь.
2. График функции.
График — часть параболы, расположенная в первой четверти, так как \(r > 0\) и \(S> 0\), точка с координатами \((0; 0)\) которой является выколотой. Функция возрастает: при увеличении радиуса площадь увеличивается.
Вернуться к содержанию учебника