Упражнение 121 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник

\(y = 0,4x^{2} \)

\(y = -0,4x^{2} \) 

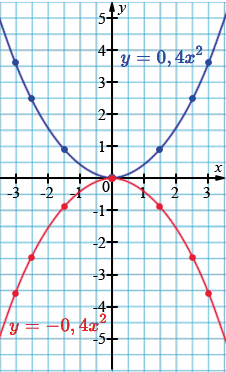
Область значений.

1) Для функции \(y = 0,4x^{2}\): \([0; +\infty) \)

2) Для функции \(y = -0,4x^{2}\): \((-\infty; 0] \)

Пояснения:

1. Вид функций.

Обе функции являются квадратичными, и потому их графики — параболы. Знак коэффициента при \(x^2\) определяет направление ветвей:

\(0,4 > 0 \Rightarrow\) ветви вверх

\( -0,4 < 0 \Rightarrow \) ветви вниз.

2. Область значений квадратичных функций.

\[ y = ax^{2} \Rightarrow \begin{cases} y \ge 0, & \text{если } a>0,\\ y \le 0, & \text{если } a<0. \end{cases} \]

Это следует из того, что \(x^{2} \ge 0\) при любых \(x\), и знак коэффициента \(a\) определяет знак произведения.

Таким образом:

— парабола \(y = 0,4x^{2}\) принимает только неотрицательные значения;

— парабола \(y = -0,4x^{2}\) принимает только неположительные значения.

а) \( y = x^{2} - 4x + 7\)

\(a = 1\), \(b = -4\), \(c=7\).

\( m = -\frac{b}{2a} = -\frac{-4}{2\cdot 1} = 2. \)

\( n = 2^{2} - 4\cdot 2 + 7 = 4 - 8 + 7 = 3\)

Вершина параболы: \((2; \,3)\).

Прямая \(x=2\) - ось симметрии параболы.

Так как \(a = 1 > 0\), ветви направлены вверх.

При \(x=0\):

\( y = 0^{2} - 4\cdot0 + 7=7.\)

Точка пересечения с осью ординат: \((0; 7)\)

б) \( y = -2x^{2} - 5x - 2 \)

\(a = -2\), \(b = -5\), \(c=-2\).

\(m= -\frac{b}{2a} = -\frac{-5}{2(-2)} = \frac{5}{-4} =\)

\(=-\frac{5}{4}\)

\(n= -2\left(-\frac{5}{4}\right)^2 - 5\left(-\frac{5}{4}\right) - 2 =\)

\(= -2\cdot\frac{25}{16} -+\frac{25}{4}^{\color{red}{\backslash{2}} } - 2 =\)

\(= -\frac{25}{8} + \frac{50}{8} - 2 = \frac{25}{8} - 2 =\)

\(=\frac{25}{8} - \frac{16}{8} = \frac{9}{8}\)

Вершина: \(\left(-\frac{5}{4};\,\frac{9}{8}\right)\).

Прямая \(x=-\frac54\) - ось симметрии параболы.

Так как \(a = -2 < 0\), ветви направлены вниз.

При \(x=0\):

\( y = -2\cdot0^{2} - 5\cdot0 - 2 = -2.\)

Точка пересечения с осью ординат: \((0; -2)\)

Пояснения:

1. Формула вершины параболы \((m; n)\):

\[ m = -\frac{b}{2a},\qquad n = f(m). \]

Это справедливо для любой функции вида \[ y = ax^2 + bx + c. \]

2. Ось симметрии

Ось симметрии — вертикальная прямая: \( x = m\).

3. Направление ветвей

• если \(a > 0\) — ветви вверх;

• если \(a < 0\) — ветви вниз.

В задаче:

а) вершина \((2,3)\), ветви вверх;

б) вершина \(\left(-\frac54; \frac98\right)\), ветви вниз.