Упражнение 816 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

Составим уравнение:

\( \frac{120}{x} = 0,75 + 0,25 + \frac{120 - 0,75x}{x+5}\)

\( \frac{120}{x} = 1 + \frac{120 - 0,75x}{x+5}\) \(/\times x(x+5)\)

ОДЗ: \(x\neq0\)   и   \(x + 5\neq 0\)

                            \(x\neq-5\)

\(120(x+5) = x(x+5) + x\left(120 - 0,75x\right)\)

\( 120x + 600 = x^2 + 5x + 120x - 0,75x^2\)

\(120x + 600 = 0,25x^2 + 125x\)

\(0,25x^2 + 125x - 120x - 600 = 0\)

\(0,25x^2 + 5x - 600 = 0\)   \(/\times 4\)

\( x^2 + 20x - 2400 = 0\)

\(a = 1\),  \(b = 20\),  \(c = -2400\)

\(D =b^2-4ac=\)

\(=20^2 - 4 \cdot 1 \cdot (-2400) =\)

\(=400 + 9600 = 10000\),

\(\sqrt{D} = 100.\)

\( x_1 = \frac{-20 + 100}{2}=\frac{80}{2} = 40\)

\( x_2 = \frac{-20 - 100}{2}=\frac{-120}{2} = -60\) - не удовлетворяет условию.

Ответ: скорость первого автомобиля равна 40 км/ч.

Пояснения:

Время в пути вычисляется по формуле \[t=\frac{S}{v}.\]

Мы обозначили скорость первого автомобиля \(x\). Так как второй автомобиль ехал сначала с этой же скоростью, потом остановился и ускорился, составили дробное рациональное уравнение по времени:

\( \frac{120}{x} = 0,75 + 0,25 + \frac{120 - 0,75x}{x+5}\).

Алгоритм решения дробного рационального уравнений:

1) найти ОДЗ (область допустимых значений), то есть те значения переменной, при которых знаменатель обращается в нуль;

2) найти общий знаменатель дробей, входящих в уравнение;

3) умножить обе части уравнения на общий знаменатель;

4) решить получившееся целое уравнение;

5) исключить из его корней те, которые совпадают с ОДЗ.

После того как обе части уравнения домножили на общий знаменатель и выполнили преобразования, получили квадратное уравнение, у которого дискриминант \(D = b^2 - 4ac>0\), поэтому уравнение имеет два корня: \(40\) и \(-60\). Но отрицательный корень не подходит, так как скорость может быть только положительным числом. Значит, скорость первого автомобиля равна 40 км/ч.

а) \(-1,5 \leq x \leq 4\)

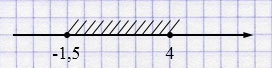
б) \(-2 < x < 1,3\)

в) \(-5 \leq x \leq -3 \frac{1}{3}\)

г) \(2 < x \leq 6,1\)

Пояснения:

Двойное неравенство ограничивает \(x\) с двух сторон.

Правила:

Если в неравенстве используется \(\leq\) или \(\geq\), то соответствующая граница включается и отмечается закрашенной точкой.

Если используется строгий знак \(<\) или \(>\), то граница не включается и отмечается пустым кружком.