Упражнение 106 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№106 учебника 2023-2025 (стр. 29):
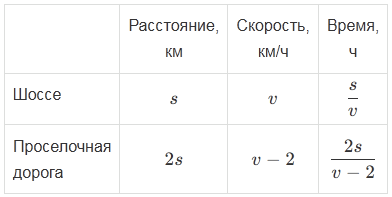
Туристы прошли \(s\) км по шоссе со скоростью \(v\) км/ч и вдвое больший путь по просёлочной дороге. Сколько времени \(t\) ч затратили туристы, если известно, что по просёлочной дороге они шли со скоростью, на 2 км/ч меньшей, чем по шоссе? Найдите \(t\) при \(s=10\), \(v=6\).
№106 учебника 2013-2022 (стр. 27):
Постройте графики функций \(y=-4x+1\) и \(y=2x-3\) и найдите координаты точки их пересечения. Ту же задачу решите без построения графиков. Сравните полученные ответы.
Подсказка
№106 учебника 2023-2025 (стр. 29):
Вспомните:
- Рациональные дроби.
- Сложение и вычитание рациональных дробей с разными знаменателями.
- Основное свойство рациональной дроби.
- Подобные слагаемые.
- Вынесение общего множителя за скобки.
- Неправильные дроби.
- Смешанные числа.
- Сокращение дробей.
№106 учебника 2013-2022 (стр. 27):
Вспомните:
- График линейной функции.
- Координаты точки.
- Что называют решением системы уравнений.
- Уравнения с двумя переменными.
- Метод подстановки при решении систем уравнений.
- Линейное уравнение с одной переменной, его свойства.
- Деление и дроби.
- Сокращение дробей.
- Неправильные дроби.
- Смешанные числа, действия с ними.
- Умножение обыкновенных дробей.
- Вычитание обыкновенных дробей.
- Подобные слагаемые.
- Вычитание рациональных чисел.
- Деление рациональных чисел.
Ответ
№106 учебника 2023-2025 (стр. 29):
\( t = \frac{s}{v} ^{\color{blue}{\backslash{}v-2}} + \frac{2s}{v-2} ^{\color{blue}{\backslash{v}}} =\)
\(= \frac{s(v-2) + 2s\,v}{v(v-2)} =\)
\(=\frac{s\,(v-2 + 2v)}{v(v-2)} = \frac{s\,(3v-2)}{v(v-2)}. \)
Если \(s=10\), \(v=6\), то
\( t = \frac{10\cdot(3\cdot6 - 2)}{6\,(6-2)} =\)
\(=\frac{10\cdot(18 - 2)}{6\cdot4} = \frac{10\cdot\cancel{16} ^2}{\cancel{24}_3} =\)
\(=\frac{20}{3}\text{ ч} = 6\frac23\text{ ч}=6\text{ ч} \, 40 \text{ мин} \)
Ответ: \(t = 6\text{ ч} \, 40 \text{ мин} \).
Пояснения:
— Время движения равно отношению пути к скорости: \(t = \tfrac{\text{расстояние}}{\text{скорость}}\).
— Общий путь складывается из времени на каждом участке.
— Для сложения и вычитания дробей приводим их к общему знаменателю, умножая числитель и знаменатель каждой дроби на необходимые множители.
— После приведения к общему знаменателю выполняем вычитание или сложение числителей, раскрывая скобки и приводя подобные члены.
— После преобразований подставляем вместо переменных
№106 учебника 2013-2022 (стр. 27):
1) \(y=-4x+1\)
| \(x\) | 0 | 1 |
| \(y\) | 1 | -3 |
\(y=2x-3\)
| \(x\) | 0 | 2 |
| \(y\) | -3 | 1 |
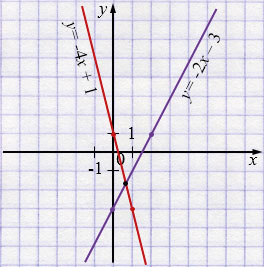
\((0,7; -1,7)\) - координаты точки пересечения прямых.
2. Составим систему:
\( \begin{cases} y=-4x+1,\\ y=2x-3. \end{cases} \)
\( -4x+1=2x-3 \)
\( -2x-4x = -3-1 \)
\( -6x=-4 \)
\(x=\frac{4}{6} \)
\(x=\frac{2}{3} \)
\( y=2\cdot\frac{2}{3}-3 =\frac{4}{3}-3 =\)
\(=1\frac13-3=-(3-1\frac13)=\)
\(=-(2\frac33-1\frac13)=-1\frac23. \)
\(\bigl(\frac23,\,-1\frac23\bigr)\) - координаты точки пересечения прямых.
При построении графиков координаты точки имеют не совсем точные значения.
Пояснения:
— Графический метод даёт наглядное представление, но его точность ограничена масштабом рисунка, получаются приближенные значения.
— Алгебраический метод (с помощью системы) точен и сразу ведёт к простому линейному уравнению.
При решении системы используем метод подстановки. Приравниваем правые части уравнений функций, получаем уравнение с одной переменной, решив которое находим значение переменной \(x\), а затем подставляя значение \(x\) в одной из уравнений находим значение переменной \(y\).
Вернуться к содержанию учебника