Упражнение 1199 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник. Страница 233
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1199 учебника 2023-2025 (стр. 233):
За 8 дней работы на первом станке и 5 дней работы на втором было изготовлено 235 деталей. В результате усовершенствования производительность первого станка возросла на 15%, а второго — на 20%. Теперь за 2 дня работы на первом станке и 3 дня на втором можно изготовить 100 деталей. Сколько деталей в день изготовляли раньше на каждом станке?
№1199 учебника 2013-2022 (стр. 233):
Постройте график уравнения:
а) \((x - 2)(y + 3) = 0\);
б) \(x^2 + x y = 0.\)
Подсказка
№1199 учебника 2023-2025 (стр. 233):
Вспомните:
- Решение задач с помощью систем уравнений.
- Что называют решением системы уравнений.
- Проценты.
- Уравнения с двумя переменными, их свойства.
- Способ подстановки при решении систем уравнений.
- Линейное уравнение с одной переменной, его свойства.
- Деление и дроби.
- Подобные слагаемые.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Деление рациональных чисел.
- Умножение десятичных дробей.
- Деление десятичных дробей.
- Сложение и вычитание десятичных дробей.
- Распределительное свойство умножения.
№1199 учебника 2013-2022 (стр. 233):
Вспомните:
- График линейной функции.
- Координаты точки.
- Уравнения с двумя переменными, их свойства.
- Линейное уравнение с одной переменной, его свойства.
- Вынесение общего множителя за скобки.
- Свойства умножения.
Ответ
№1199 учебника 2023-2025 (стр. 233):
15% = 0,15;
20% = 0,2.
Пусть \(x\) деталей в день изготавливал первый станок, \(y\) деталей в день — второй станок. Тогда первый станок стал изготавливать
\(x + 0,15x = 1,15x\) деталей, а второй — \(y + 0,2y = 1,2y\) деталей.
Составим систему уравнений:
\( \begin{cases} 8x + 5y = 235, / : 5 \\2\cdot1{,}15x + 3\cdot1{,}2y = 100 \end{cases} \)
\( \begin{cases} 1,6x + y = 47,\\ 2,3x + 3,6y = 100 \end{cases} \)
\( \begin{cases} y = 47 - 1,6x,\\ 2,3x + 3,6(47 - 1,6x) = 100 \end{cases} \)
\(2,3x + 3,6(47 - 1,6x) = 100\)
\(2,3x + 169,2 - 5,76x = 100\)
\(-3,46x = 100 - 169,2\)
\(-3,46x = -69,2\)
\(x = \frac{69,2}{3,46}\)
\(x = 20\)
\(y = 47 - 1,6\cdot20 = 47 - 32 = 15\)
|
|
Ответ: 20 деталей в день изготовляли на первом станке, 15 деталей в день — на втором.
Пояснения:
– Вводим переменные \(x\) и \(y\) как исходные дневные нормы станков.
– Первое уравнение отражает общий выпуск до модернизации.
– Второе уравнение учитывает увеличение производительности на 15% и 20% и новую норму выпуска за 2 и 3 дня.
– Решение системы методом подстановки:
- из одного уравнения выражаем одну переменную через другую;
- подставляем это выражение в другое уравнение, получая уравнение с одной переменной;
- решаем полученное уравнение, находим значение первой переменной;
- затем вычисляем вторую переменную, подставляя найденное значение обратно.
№1199 учебника 2013-2022 (стр. 233):
а) \((x - 2)(y + 3) = 0\)
1) \(x - 2 = 0\)
\(x = 2\).
2) \(y + 3 = 0\).
\(y = -3\).

б) \(x^2 + x y = 0\)
\( x(x + y) = 0 \)
1) \(x = 0\) - ось \(y\).
2) \(x + y = 0\).
\(y = -x\)
| \(x\) | 0 | 3 |
| \(y\) | 0 | -3 |
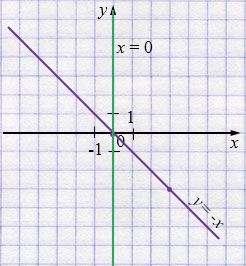
Пояснения:
Уравнение вида произведения равно нулю разбивается на несколько линейных уравнений, каждое задаёт прямую.
а) Уравнение \((x - 2)(y + 3) = 0\) означает, что либо \(x - 2 = 0\), либо \(y + 3 = 0\).
— Прямая \(x = 2\);
— Прямая \(y = -3\).
Получились две перпендикулярные прямые \(x=2\) - вертикальная прямая и \(y=-3\) - горизонтальная прямая.
б) Уравнение \(x^2 + x y = 0\) можно разложить:
\( x(x + y) = 0 \)
Значит либо \(x = 0\), либо \(x + y = 0\).
— Прямая \(x = 0\) (ось \(y\));
— Прямая \(y = -x\).
График: прямые \(x=0\), то есть ось \(y\), и \(y=-x\) пересекаются в начале координат.
Вернуться к содержанию учебника