Упражнение 1091 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1091 учебника 2023-2025 (стр. 216):
Найдите решение системы уравнений:
а) \( \begin{cases} 3(x - 5) - 1 = 6 - 2x,\\ 3(x - y) - 7y = -4; \end{cases} \)
б) \( \begin{cases} 6(x + y) - y = -1,\\ 7(y + 4) - (y + 2) = 0. \end{cases} \)
№1091 учебника 2013-2022 (стр. 218):
Задайте формулой линейную функцию, график которой изображён на рисунке 81:
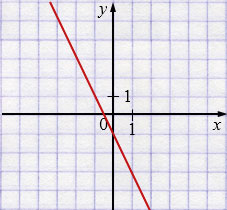
Рис. 81
Подсказка
№1091 учебника 2023-2025 (стр. 216):
Вспомните:
- Что значит решить систему уравнений.
- Способ подстановки при решении систем уравнений.
- Свойства уравнений.
- Линейное уравнение.
- Деление и дроби.
- Неправильные дроби.
- Смешанные числа.
- Подобные слагаемые.
- Умножение обыкновенных дробей.
- Умножение десятичных дробей.
- Деление десятичных дробей.
- Сложение десятичных дробей.
- Распределительное свойство умножения.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Умножение рациональных чисел.
- Деление рациональных чисел.
№1091 учебника 2013-2022 (стр. 218):
Вспомните:
- График линейной функции.
- Координаты точки.
- Что называют решением системы уравнений.
- Способ подстановки при решении систем уравнений.
- Линейное уравнение.
- Свойства уравнений.
Ответ
№1091 учебника 2023-2025 (стр. 216):
а) \( \begin{cases} 3(x - 5) - 1 = 6 - 2x,\\ 3(x - y) - 7y = -4; \end{cases} \)
\( \begin{cases} 3x - 15 - 1 = 6 - 2x,\\ 3x - 3y - 7y = -4; \end{cases} \)
\( \begin{cases} 3x + 2x = 6 + 16,\\ 3x - 10y = -4; \end{cases} \)
\( \begin{cases} 5x = 22,\\ 3x - 10y = -4; \end{cases} \)
\( \begin{cases} x = \tfrac{22}{5},\\ 3x - 10y = -4; \end{cases} \)
\( \begin{cases} x = 4,4,\\ 3x - 10y = -4; \end{cases} \)
\( \begin{cases} x = 4,4,\\ 3\cdot4,4 - 10y = -4; \end{cases} \)
\( \begin{cases} x = 4,4,\\ 13,2 - 10y = -4; \end{cases} \)
\( \begin{cases} x = 4,4,\\ 10y = 13,2+4; \end{cases} \)
\( \begin{cases} x = 4,4,\\ 10y = 17,2; \end{cases} \)
\( \begin{cases} x = 4,4,\\ y = \tfrac{17,2}{10}; \end{cases} \)
\( \begin{cases} x = 4,4,\\ y =1,72. \end{cases} \)
Ответ: \(x = 4,4\), \( y =1,72\).
б) \( \begin{cases} 6(x + y) - y = -1,\\ 7(y + 4) - (y + 2) = 0; \end{cases} \)
\( \begin{cases} 6x + 6y - y = -1,\\ 7y + 28 - y - 2 = 0; \end{cases} \)
\( \begin{cases} 6x + 5y= -1,\\ 6y + 26 = 0; \end{cases} \)
\( \begin{cases} 6x + 5y= -1,\\ 6y = -26; \end{cases} \)
\( \begin{cases} 6x + 5y= -1,\\ y = -\tfrac{26}{6}; \end{cases} \)
\( \begin{cases} 6x + 5y= -1,\\ y = -\tfrac{13}{3}; \end{cases} \)
\( \begin{cases} 6x + 5\cdot(-\frac{13}{3})= -1,\\ y = -\tfrac{13}{3}; \end{cases} \)
\( \begin{cases} 6x - \frac{65}{3}= -1, /\times3 \\ y = -\tfrac{13}{3}; \end{cases} \)
\( \begin{cases} 18x - 65= -3, \\ y = -\tfrac{13}{3}; \end{cases} \)
\( \begin{cases} 18x = -3 + 65, \\ y = -\tfrac{13}{3}; \end{cases} \)
\( \begin{cases} 18x = 62, \\ y = -\tfrac{13}{3}; \end{cases} \)
\( \begin{cases} x = \tfrac{62}{18}, \\ y = -\tfrac{13}{3}; \end{cases} \)
\( \begin{cases} x = \tfrac{31}{9}, \\ y = -\tfrac{13}{3}; \end{cases} \)
\( \begin{cases} x = 3\tfrac{4}{9}, \\ y = -4\tfrac{1}{3}; \end{cases} \)
Ответ: \(x = 3\tfrac{4}{9}\), \(y = -4\tfrac{1}{3}\).
Пояснения:
Использован метод подстановки:
1. В каждом уравнении раскрываем скобки, используя распределительное свойство умножения, и приводим подобные.
2. Из одного уравнения находим одну из переменных.
3. Подставляем найденное значение в другое уравнение, и, решив полученное уравнение, находим вторую переменную.
№1091 учебника 2013-2022 (стр. 218):
\((0; -1)\) и \((-1;1)\).
\(y = kx + b\)
\( \begin{cases} -1 = k\cdot0 + b,\\ 1 = k\cdot(-1) + b. \end{cases} \)
\( \begin{cases} b = -1,\\ 1 = -k + b. \end{cases} \)
\( \begin{cases} b = -1,\\ k = b - 1. \end{cases} \)
\( \begin{cases} b = -1,\\ k = -1 - 1. \end{cases} \)
\( \begin{cases} b = -1,\\ k = -2. \end{cases} \)
\( y = -2x - 1. \)
Ответ: \( y = -2x - 1. \)
Пояснения:
Использованные приёмы:
1) Уравнение линейной функции
\(y=kx+b\).
2) Составление системы из двух уравнений
\(\;y_1 = kx_1 + b,\;y_2 = kx_2 + b\),
где \((x_1; y_1)\) и \((x_2; y_2)\) - координаты точек на прямой.
3) Подстановка: после нахождения одной переменной подставляем её значение в одно из исходных уравнений для вычисления значения второй переменной.
Вернуться к содержанию учебника