Задание 408 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№408 учебника 2013-2022 (стр. 112):
Докажите, что параллелограмм является ромбом, если: а) его диагонали взаимно перпендикулярны; б) диагональ делит его угол пополам.
№408 учебника 2023-2024 (стр. 115):
Подсказка
№408 учебника 2013-2022 (стр. 112):
Вспомните:
- Что такое треугольник.
- Какие треугольники называются равными.
- Какой треугольник называется прямоугольным.
- Признаки равенства прямоугольных треугольников.
- Какой треугольник называется равнобедренным.
- Свойства равнобедренного треугольника.
- Что такое параллелограмм.
- Что такое ромб.
- Что такое биссектриса угла.
№408 учебника 2023-2024 (стр. 115):
Вспомните:
- Что называют окружностью, ее диаметр, хорды.
- Какие фигуры называют симметричными относительно прямой.
- Какой треугольник называется равнобедренным.
- Свойства равнобедренного треугольника.
- Свойства равных треугольников.
- Признак равнобедренного треугольника.
- Биссектриса, медиана и высота треугольника.
- Что называют серединным перпендикуляром к отрезку.
- Третий признак равенства треугольников.
Ответ
№408 учебника 2013-2022 (стр. 112):
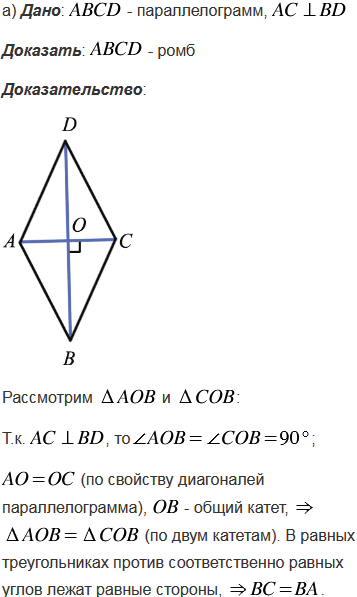
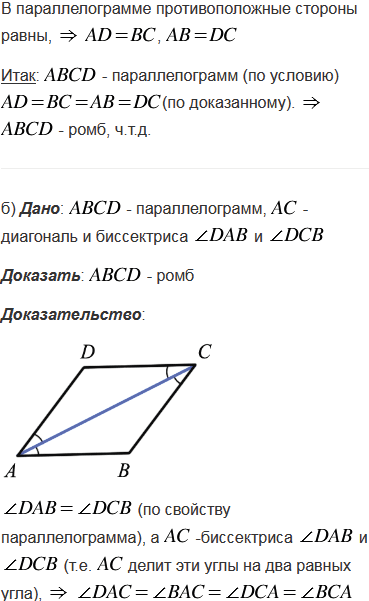



№408 учебника 2023-2024 (стр. 115):
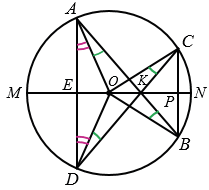
Дано: окр.(О), АВ и СD - хорды,
АВ = СD, МN - диаметр, АВ 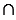 СD = К,
СD = К,
К 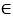 МN.
МN.
Доказать: АВ и СD симметричны относительно МN.
Доказательство:
1. К 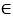 МN,
МN, 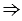 K симметрична сама себе относительно МN.
K симметрична сама себе относительно МN.
2. 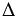 АОВ =
АОВ = 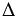 COD по трем сторонам (ОА = ОВ = ОС = ОD - радиусы, АВ = СD по условию),
COD по трем сторонам (ОА = ОВ = ОС = ОD - радиусы, АВ = СD по условию), 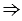
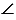 ОАВ =
ОАВ = 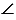 ОDС.
ОDС.
3. 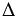 АОD - равнобедренный (ОА = ОD - радиусы),
АОD - равнобедренный (ОА = ОD - радиусы), 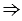
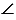 ОАD =
ОАD = 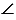 ОDА (углы при основании).
ОDА (углы при основании).
4. 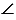 DАВ =
DАВ = 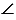 ОАD +
ОАD + 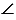 ОАВ,
ОАВ,
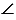 АDС =
АDС = 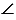 ОDА +
ОDА + 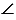 ОDС,
ОDС, 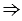
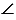 DАВ =
DАВ = 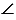 АDС,
АDС, 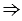
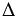 АKD - равнобедренный (признак равнобедренного треугольника),
АKD - равнобедренный (признак равнобедренного треугольника), 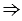 АK = KD,
АK = KD, 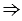 СК = KB (т.к. по условию АВ = СD).
СК = KB (т.к. по условию АВ = СD).
5. ОС = ОВ (радиусы), ОK - общая, СK = KB, 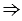
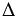 ОСК =
ОСК = 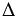 ОВК,
ОВК, 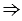
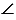 СОК =
СОК = 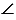 ВОК,
ВОК, 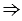 ОР - биссектриса равнобедренного
ОР - биссектриса равнобедренного 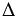 ВОС,
ВОС, 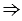 ОР - высота и медиана
ОР - высота и медиана 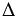 ВОС (свойство равнобедренного треугольника),
ВОС (свойство равнобедренного треугольника), 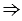 ОР, значит, и МN - серединный перпендикуляр к отрезку ВС,
ОР, значит, и МN - серединный перпендикуляр к отрезку ВС, 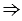 точки В и С симметричны относительно МN.
точки В и С симметричны относительно МN.
6. Точка К симметрична относительно МN, точки В и С симметричны относительно МN, 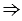 хорды АВ и СD симметричны относительно МN. Что и требовалось доказать.
хорды АВ и СD симметричны относительно МN. Что и требовалось доказать.
Пояснения:
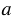 , если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему. Прямая
, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему. Прямая 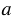 называется осью симметрии точек A и A1. Каждая точка оси
называется осью симметрии точек A и A1. Каждая точка оси 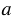 симметрична самой себе.
симметрична самой себе.Прямая однозначно задается двумя точками, следовательно, для доказательства симметричности двух прямых относительно прямой, нам нужно доказать симметричность двух точек одной прямой к двум точкам другой прямой.
Вернуться к содержанию учебника