Задание 411 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№411 учебника 2013-2022 (стр. 112):
В прямоугольном треугольнике проведена биссектриса прямого угла. Через точку пересечения этой биссектрисы с гипотенузой проведены прямые, параллельные катетам. Докажите, что полученный четырёхугольник - квадрат.
№411 учебника 2023-2024 (стр. 115):
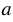 , b и окружность с центром О. а) Постройте прямую
, b и окружность с центром О. а) Постройте прямую 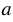 1, симметричную прямой
1, симметричную прямой 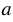 относительно прямой b. б) Используя прямую
относительно прямой b. б) Используя прямую 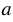 1, постройте отрезок так, чтобы прямая b была серединным перпендикуляром к этому отрезку и чтобы концы этого отрезка лежали соответственно на прямой
1, постройте отрезок так, чтобы прямая b была серединным перпендикуляром к этому отрезку и чтобы концы этого отрезка лежали соответственно на прямой 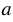 и данной окружности.
и данной окружности.Подсказка
№411 учебника 2013-2022 (стр. 112):
Вспомните:
- Какой треугольник называется прямоугольным.
- Что такое биссектриса.
- Что такое параллелограмм.
- Что такое прямоугольник.
- Что такое ромб.
- Что такое квадрат.
№411 учебника 2023-2024 (стр. 115):
Вспомните:
- Какие фигуры называют симметричными относительно прямой.
- Что называют серединным перпендикуляром к отрезку.
- Окружность, ее элементы.
Ответ
№411 учебника 2013-2022 (стр. 112):
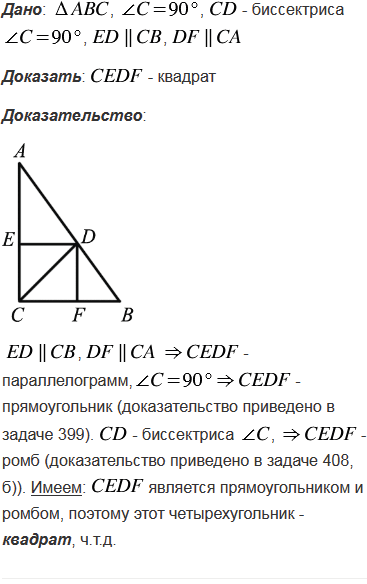


№411 учебника 2023-2024 (стр. 115):
Дано: прямые  , b и окр. (О).
, b и окр. (О).
Построить: а) прямую  1, симметричную прямой
1, симметричную прямой  относительно прямой b. б) Используя прямую
относительно прямой b. б) Используя прямую  1, постройте отрезок так, чтобы прямая b была серединным перпендикуляром к этому отрезку и чтобы концы этого отрезка лежали соответственно на прямой
1, постройте отрезок так, чтобы прямая b была серединным перпендикуляром к этому отрезку и чтобы концы этого отрезка лежали соответственно на прямой  и данной окружности.
и данной окружности.
Решение:
1 случай
а)
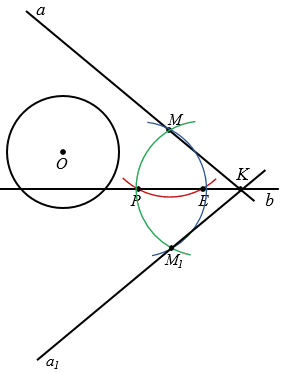
Точка К симметрична сама себе относительно b, точка М1 по построению симметрична М относительно b, 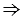
 1 симметрична
1 симметрична  относительно b.
относительно b.
б) Невозможно построить.
2 случай
а)
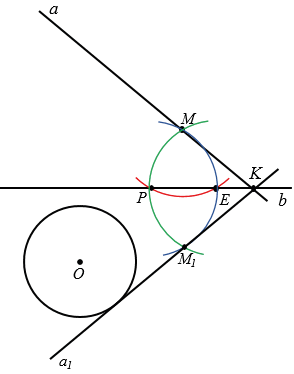
Точка К симметрична сама себе относительно b, точка М1 по построению симметрична М относительно b, 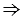
 1 симметрична
1 симметрична  относительно b.
относительно b.
б)
Точки С и С1 по построению симметричны относительно b,  прямая b - серединный перпендикуляр к отрезку СС1.
прямая b - серединный перпендикуляр к отрезку СС1.
3 случай
а)
Точка К симметрична сама себе относительно b, точка М1 по построению симметрична М относительно b, 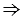
 1 симметрична
1 симметрична  относительно b.
относительно b.
б)
Точки С и С1 по построению симметричны относительно b,  прямая b - серединный перпендикуляр к отрезку СС1.
прямая b - серединный перпендикуляр к отрезку СС1.
Точки Н и Н1 по построению симметричны относительно b, 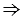 прямая b - серединный перпендикуляр к отрезку РР1.
прямая b - серединный перпендикуляр к отрезку РР1.
Пояснения:
Две фигуры называются симметричными относительно прямой, если каждая точка одной фигуры симметрична некоторой точке другой фигуры, и обратно. Данная прямая называется осью симметрии этих фигур. Две точки А и А1 называются симметричными относительно прямой  , если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему. Прямая
, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему. Прямая  называется осью симметрии точек A и A1. Каждая точка оси
называется осью симметрии точек A и A1. Каждая точка оси  симметрична самой себе.
симметрична самой себе.
1 случай
Прямая  1 и окружность не будут иметь общих точек.
1 и окружность не будут иметь общих точек.
а) Нам даны две прямые  , b и окружность с центром О. Чертим их.
, b и окружность с центром О. Чертим их.
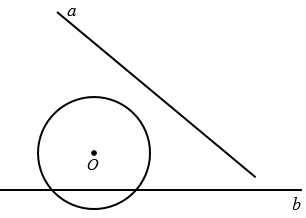
Прямая однозначно задается двумя точками, поэтому, чтобы построить прямую  1, симметричную прямой
1, симметричную прямой  относительно b, нужно двум точкам лежащим на прямой
относительно b, нужно двум точкам лежащим на прямой  построить две симметричные точки относительно прямой b, через которые и пройдет прямая
построить две симметричные точки относительно прямой b, через которые и пройдет прямая  1.
1.
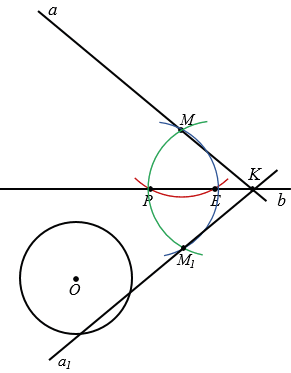
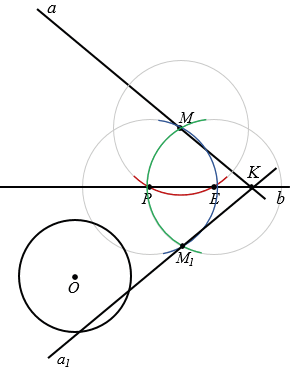
Точка пересечения прямых  и b, обозначим ее буквой K, относительно прямой р будет симметрична сама себе. Отметим точку М на прямой
и b, обозначим ее буквой K, относительно прямой р будет симметрична сама себе. Отметим точку М на прямой  и построим точку М1, симметричную ей относительно b. Для этого строим с помощью циркуля окружность с центром М так, чтобы она пересекла прямую b в двух точках, обозначим их Р и Е (полностью окружность строить необязательно, смотри выделенное красным цветом). Далее строим две окружности с центрами в точках Р и Е так, чтобы каждая из них проходила через точку М (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом). Эти окружности пересекутся в двух точках, одна из них точка М, а друга точка М1, которая и будет симметрична точке М относительно b. Через точки К и М1 проводим прямую
и построим точку М1, симметричную ей относительно b. Для этого строим с помощью циркуля окружность с центром М так, чтобы она пересекла прямую b в двух точках, обозначим их Р и Е (полностью окружность строить необязательно, смотри выделенное красным цветом). Далее строим две окружности с центрами в точках Р и Е так, чтобы каждая из них проходила через точку М (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом). Эти окружности пересекутся в двух точках, одна из них точка М, а друга точка М1, которая и будет симметрична точке М относительно b. Через точки К и М1 проводим прямую  1, симметричную прямой
1, симметричную прямой  относительно b.
относительно b.
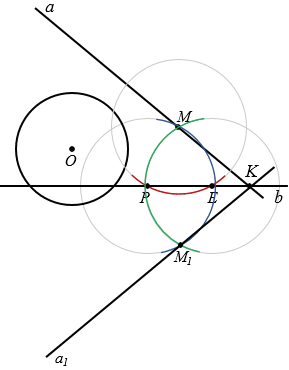
б) В рассматриваемом случае, когда прямая  1 и окружность не имеют общих точек, построить отрезок такой, чтобы прямая b была серединным перпендикуляром к этому отрезку и чтобы концы этого отрезка лежали соответственно на прямой
1 и окружность не имеют общих точек, построить отрезок такой, чтобы прямая b была серединным перпендикуляром к этому отрезку и чтобы концы этого отрезка лежали соответственно на прямой  и данной окружности, нельзя.
и данной окружности, нельзя.
2 случай
Прямая  1 и окружность будут иметь одну общую точку, для этого меняем расположение прямых
1 и окружность будут иметь одну общую точку, для этого меняем расположение прямых  , b и окружности.
, b и окружности.
а) Прямую  1, симметричную прямой
1, симметричную прямой  , относительно b, строим по алгоритму, приведенному в первом случае.
, относительно b, строим по алгоритму, приведенному в первом случае.
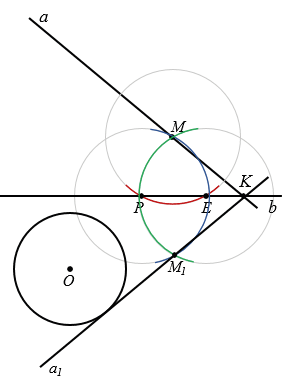
б) У нас получилось, что прямая  1 и окружность имеют одну общую точку, обозначим эту точку буквой С1. Точка С1 лежит на окружности, при этом она симметрична какой-то из точек, лежащей на прямой
1 и окружность имеют одну общую точку, обозначим эту точку буквой С1. Точка С1 лежит на окружности, при этом она симметрична какой-то из точек, лежащей на прямой  , относительно b, так как по построению прямые
, относительно b, так как по построению прямые  и
и  1 симметричны относительно прямой b. Построим эту точку.
1 симметричны относительно прямой b. Построим эту точку.
Сначала строим с помощью циркуля окружность с центром С1 так, чтобы она пересекла прямую b в двух точках, обозначим их D и F (полностью окружность строить необязательно, смотри выделенное коричневым цветом). Далее строим две окружности с центрами в точках D и F так, чтобы каждая из них проходила через точку C1 (полностью окружности строить необязательно, смотри выделенное фиолетовым и желтым цветом). Эти окружности пересекутся в двух точках, одна из них точка C1, а другая - точка C, которая и будет симметрична точке C1 относительно b. Соединяем точки C и C1 и получаем отрезок CC1, у которого концы лежат соответственно на прямой  и данной окружности и прямая b ось симметрии отрезка CC1.
и данной окружности и прямая b ось симметрии отрезка CC1.
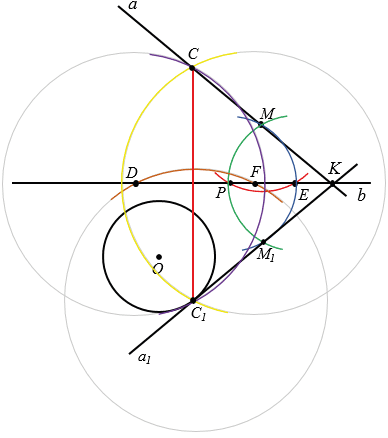
3 случай
Прямая  1 и окружность будут иметь две общие точки, для этого меняем расположение прямых
1 и окружность будут иметь две общие точки, для этого меняем расположение прямых  , b и окружности.
, b и окружности.
а) Прямую  1, симметричную прямой
1, симметричную прямой  , относительно b, строим по алгоритму, приведенному в первом случае.
, относительно b, строим по алгоритму, приведенному в первом случае.
б) У нас получилось, что прямая  1 и окружность имеют две общие точки, обозначим эти точку буквой С1 и H1. Точки С1 и H1 лежит на окружности, при этом они симметричны каким-то двум точкам, лежащим на прямой
1 и окружность имеют две общие точки, обозначим эти точку буквой С1 и H1. Точки С1 и H1 лежит на окружности, при этом они симметричны каким-то двум точкам, лежащим на прямой  , относительно b, так как по построению прямые
, относительно b, так как по построению прямые  и
и  1 симметричны относительно прямой b. Построим эти точки.
1 симметричны относительно прямой b. Построим эти точки.
Сначала построим точку С, симметричную точке С1, для этого строим с помощью циркуля окружность с центром С1 так, чтобы она пересекла прямую b в двух точках, обозначим их D и F (полностью окружность строить необязательно, смотри выделенное коричневым цветом). Далее строим две окружности с центрами в точках D и F так, чтобы каждая из них проходила через точку C1 (полностью окружности строить необязательно, смотри выделенное фиолетовым и желтым цветом). Эти окружности пересекутся в двух точках, одна из них точка C1, а другая - точка C, которая и будет симметрична точке C1 относительно b. Соединяем точки C и C1 и получаем отрезок CC1, у которого концы лежат соответственно на прямой  и данной окружности и прямая b ось симметрии отрезка CC1.
и данной окружности и прямая b ось симметрии отрезка CC1.
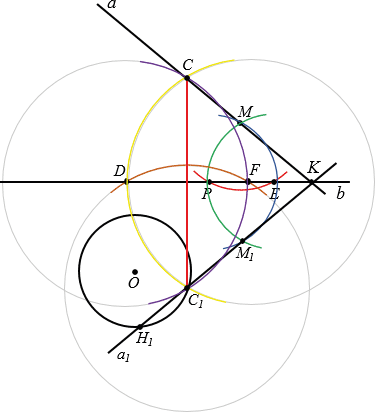
Затем по алгоритму построения отрезка СС1 строим отрезок НН1, у которого концы лежат соответственно на прямой  и данной окружности и прямая b ось симметрии отрезка НН1.
и данной окружности и прямая b ось симметрии отрезка НН1.
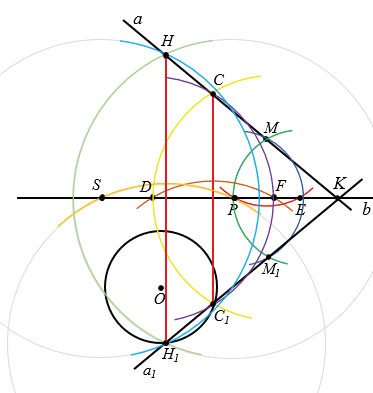
Вернуться к содержанию учебника