Задание 410 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№410 учебника 2013-2022 (стр. 112):
Является ли четырёхугольник квадратом, если его диагонали: а) равны и взаимно перпендикулярны; б) взаимно перпендикулярны и имеют общую середину; в) равны, взаимно перпендикулярны и имеют общую середину?
№410 учебника 2023-2024 (стр. 115):
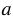 , b, p. а) Постройте прямую b1, симметричную прямой b относительно прямой p. б) Пользуясь прямой b1, постройте отрезок так, чтобы его концы лежали соответственно на прямых
, b, p. а) Постройте прямую b1, симметричную прямой b относительно прямой p. б) Пользуясь прямой b1, постройте отрезок так, чтобы его концы лежали соответственно на прямых 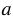 и b и чтобы прямая p была осью симметрии отрезка.
и b и чтобы прямая p была осью симметрии отрезка.Подсказка
№410 учебника 2013-2022 (стр. 112):
Вспомните:
- Что такое четырехугольник.
- Что такое диагональ.
- Что такое квадрат.
- Что такое ромб.
№410 учебника 2023-2024 (стр. 115):
Вспомните:
- Какие фигуры называют симметричными.
- Что называют отрезком.
- Как построить перпендикулярные прямые.
Ответ
№410 учебника 2013-2022 (стр. 112):



№410 учебника 2023-2024 (стр. 115):
Дано: прямые 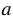 , b, p.
, b, p.
Построить: а) прямую b1, симметричную прямой b относительно прямой p;
б) пользуясь прямой b1, постройте отрезок так, чтобы его концы лежали соответственно на прямых 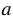 и b и чтобы прямая p была осью симметрии отрезка.
и b и чтобы прямая p была осью симметрии отрезка.
Решение:
а) b и b1 симметричны относительно р.
б) отрезок FF1 симметричен относительно оси симметрии р и F 
 , F1
, F1  b.
b.
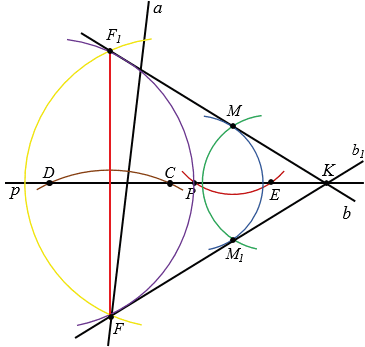
Пояснения:
Нам даны три прямые 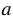 , b, p. Чертим их.
, b, p. Чертим их.
Две фигуры называются симметричными относительно прямой, если каждая точка одной фигуры симметрична некоторой точке другой фигуры, и обратно. Данная прямая называется осью симметрии этих фигур. Две точки А и А1 называются симметричными относительно прямой  , если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему. Прямая
, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему. Прямая 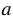 называется осью симметрии точек A и A1. Каждая точка оси
называется осью симметрии точек A и A1. Каждая точка оси 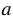 симметрична самой себе.
симметрична самой себе.
а) Прямая однозначно задается двумя точками, поэтому, чтобы построить прямую b1, симметричную прямой b относительно р, нужно двум точкам лежащим на прямой b построить две симметричные точки относительно прямой р, через которые и пройдет прямая b1.
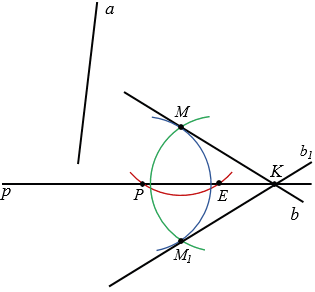
Точка пересечения прямых р и b, обозначим ее буквой K, относительно прямой р будет симметрична сама себе. Отметим точку М на прямой b и построим точку М1, симметричную ей относительно р. Для этого строим с помощью циркуля окружность с центром М так, чтобы она пересекла прямую р в двух точках, обозначим их Р и Е (полностью окружность строить необязательно, смотри выделенное красным цветом). Далее строим две окружности с центрами в точках Р и Е так, чтобы каждая из них проходила через точку М (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом). Эти окружности пересекутся в двух точках, одна из них точка М, а друга точка М1, которая и будет симметрична точке М относительно р. Через точки К и М1 проводим прямую b1, симметричную прямой b относительно р.

б) Чтобы построить отрезок, у которого концы лежат соответственно на прямых 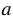 и b и чтобы прямая p была осью симметрии этого отрезка, продлим прямые
и b и чтобы прямая p была осью симметрии этого отрезка, продлим прямые 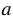 и b1 до их пересечения. Обозначим точку пересечения прямых
и b1 до их пересечения. Обозначим точку пересечения прямых 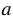 и b1 буквой F. Точка F лежит на прямой
и b1 буквой F. Точка F лежит на прямой 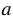 , при этом она симметрична какой-то из точек, лежащей на прямой b относительно р, так как по построению прямые b и b1 симметричны относительно прямой р. Построим эту точку.
, при этом она симметрична какой-то из точек, лежащей на прямой b относительно р, так как по построению прямые b и b1 симметричны относительно прямой р. Построим эту точку.
Сначала строим с помощью циркуля окружность с центром F так, чтобы она пересекла прямую р в двух точках, обозначим их D и C (полностью окружность строить необязательно, смотри выделенное коричневым цветом). Далее строим две окружности с центрами в точках D и C так, чтобы каждая из них проходила через точку F (полностью окружности строить необязательно, смотри выделенное фиолетовым и желтым цветом). Эти окружности пересекутся в двух точках, одна из них точка F, а другая - точка F1, которая и будет симметрична точке F относительно р. Соединяем точки F и F1 и получаем отрезок FF1, у которого концы лежат соответственно на прямых 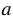 и b и прямая p ось симметрии отрезка FF1.
и b и прямая p ось симметрии отрезка FF1.

Вернуться к содержанию учебника