Задание 404 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№404 учебника 2013-2022 (стр. 112):
Докажите, что медиана прямоугольного треугольника, проведённая к гипотенузе, равна половине гипотенузы.
№404 учебника 2023-2024 (стр. 115):
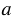 , перпендикулярны.
, перпендикулярны.Подсказка
№404 учебника 2013-2022 (стр. 112):
Вспомните:
- Какой треугольник называется прямоугольным.
- Что такое медиана.
- Что такое параллелограмм.
- Что такое прямоугольник.
- Что такое симметрия.
№404 учебника 2023-2024 (стр. 115):
Вспомните:
- Какие фигуры называют симметричными относительно прямой.
- Какие прямые называют перпендикулярными.
- Третий признак равенства треугольников.
Ответ
№404 учебника 2013-2022 (стр. 112):
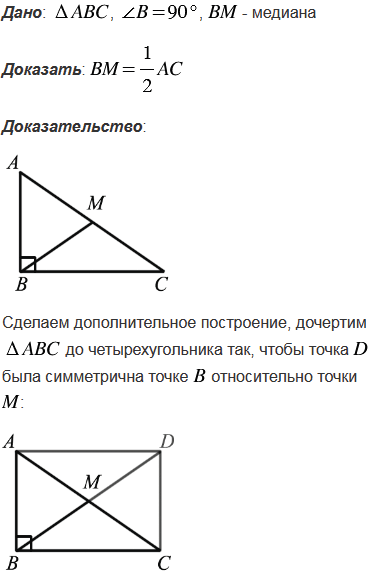


№404 учебника 2023-2024 (стр. 115):
Дано: прямые с1 и b1 симметричны прямым с и b относительно прямой 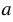 , с
, с 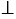 b.
b.
Доказать: с1 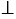 b1
b1
Доказательство:
1 случай:
Пусть b и с пересекают ось 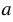 .
.
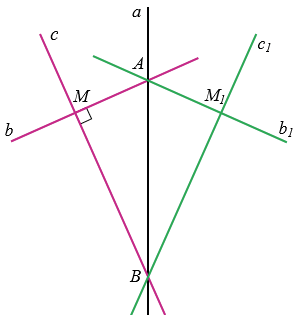
В 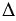 АМВ и
АМВ и 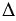 АМ1В: АВ общая, АМ = АМ1, ВМ = ВМ1 (т.к. прямые с1 и b1 симметричны прямым с и b относительно прямой
АМ1В: АВ общая, АМ = АМ1, ВМ = ВМ1 (т.к. прямые с1 и b1 симметричны прямым с и b относительно прямой 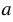 ),
), 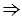
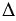 АМВ =
АМВ = 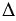 АМ1В по 3 признаку равенства треугольников,
АМ1В по 3 признаку равенства треугольников, 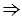
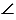 АМВ =
АМВ = 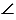 АМ1В,
АМ1В, 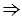 с1
с1 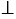 b1. Что и требовалось доказать.
b1. Что и требовалось доказать.
2 случай:
Пусть b пересекает ось 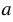 , а c не пересекает.
, а c не пересекает.
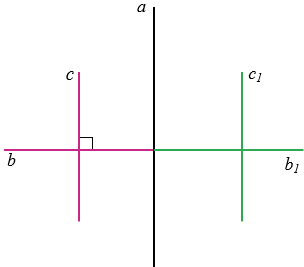
с и с1 симметричны относительно 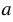 ,
, 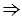 с
с 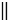 с1, а b и b1 - совпадают, при этом с
с1, а b и b1 - совпадают, при этом с 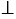 b,
b, 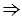 с1
с1 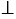 b1. Что и требовалось доказать.
b1. Что и требовалось доказать.
Пояснения:
1 случай:
Пусть обе прямые b и с пересекают ось симметрии 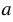 в точках А и В соответственно. Две фигуры называются симметричными относительно прямой, если каждая точка одной фигуры симметрична некоторой точке другой фигуры, и обратно. Каждая точка оси
в точках А и В соответственно. Две фигуры называются симметричными относительно прямой, если каждая точка одной фигуры симметрична некоторой точке другой фигуры, и обратно. Каждая точка оси 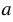 симметрична самой себе. Тогда, точки А и В симметричны сами себе соответственно, а точка М симметрична точке М1.
симметрична самой себе. Тогда, точки А и В симметричны сами себе соответственно, а точка М симметрична точке М1.
Рассмотрим 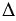 АМВ и
АМВ и 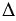 АМ1В. Сторона АВ в этих треугольниках общая, а также АМ = АМ1, ВМ = ВМ1, т.к. расстояние между двумя данными точками равно расстоянию между симметричными им точками. Следовательно,
АМ1В. Сторона АВ в этих треугольниках общая, а также АМ = АМ1, ВМ = ВМ1, т.к. расстояние между двумя данными точками равно расстоянию между симметричными им точками. Следовательно, 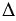 АМВ =
АМВ = 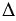 АМ1В по 3 признаку равенства треугольников (по трем сторонам). В равных треугольниках против соответственно равных сторон лежат соответственно равные углы, тогда
АМ1В по 3 признаку равенства треугольников (по трем сторонам). В равных треугольниках против соответственно равных сторон лежат соответственно равные углы, тогда 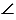 АМВ =
АМВ = 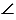 АМ1В. При этом по условию с
АМ1В. При этом по условию с 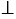 b, значит, и с1
b, значит, и с1 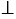 b1. Что и требовалось доказать.
b1. Что и требовалось доказать.
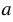 , а другая прямая c не пересекает ось
, а другая прямая c не пересекает ось 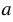 . Прямые с и с1 симметричны относительно оси
. Прямые с и с1 симметричны относительно оси 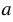 , значит, прямая с1 также не пересекает ось
, значит, прямая с1 также не пересекает ось 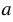 , т.е. с
, т.е. с 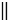 с1, т.к. если две прямые симметричны относительно оси
с1, т.к. если две прямые симметричны относительно оси 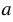 , то они либо параллельны, либо их точка пересечения лежит на оси симметрии
, то они либо параллельны, либо их точка пересечения лежит на оси симметрии 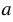 .
.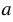 , значит, с
, значит, с 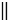
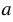 , при этом с
, при этом с 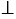 b, значит, b
b, значит, b 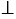
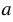 , так как если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая ей перпендикулярна, следовательно, прямая b и симметричная ей прямая b1 совпадают и b1
, так как если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая ей перпендикулярна, следовательно, прямая b и симметричная ей прямая b1 совпадают и b1 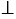 c.
c.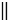 с1, b1
с1, b1 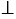 c, значит, с1
c, значит, с1 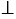 b1, так как если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая ей перпендикулярна. Что и требовалось доказать.
b1, так как если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая ей перпендикулярна. Что и требовалось доказать.Вернуться к содержанию учебника