Угол между векторами
Пусть нам даны векторы 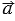 и
и 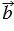 . Отложим от произвольной точки О векторы
. Отложим от произвольной точки О векторы 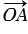 =
= 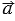 и
и 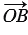 =
=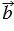 :
:
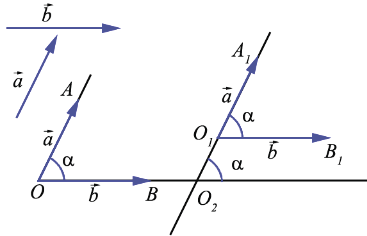
В том случае если данные векторы 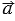 и
и 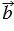 не являются сонаправленными, лучи ОА и ОВ образуют угол АОВ. Угол между векторами
не являются сонаправленными, лучи ОА и ОВ образуют угол АОВ. Угол между векторами 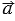 и
и 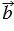 равен
равен 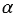 , где
, где 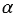 - градусная мера угла АОВ. То есть углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором. При этом
- градусная мера угла АОВ. То есть углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором. При этом 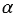 - не зависит от выбора точки О, от которой откладываются векторы
- не зависит от выбора точки О, от которой откладываются векторы 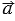 и
и 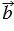 . Действительно, отложим векторы
. Действительно, отложим векторы 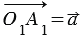 и
и 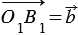 от произвольной точки О1. Мы знаем, что векторы называются равными, если они сонаправлены и их длины равны, т.е. равные векторы лежат либо на одной прямой либо на параллельных прямых, поэтому
от произвольной точки О1. Мы знаем, что векторы называются равными, если они сонаправлены и их длины равны, т.е. равные векторы лежат либо на одной прямой либо на параллельных прямых, поэтому 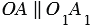 и
и 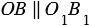 . При этом если две параллельные прямые пересечены секущей, то соответственные углы равны, значит,
. При этом если две параллельные прямые пересечены секущей, то соответственные углы равны, значит, 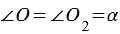 как соответственные углы при пересечении параллельных прямых
как соответственные углы при пересечении параллельных прямых 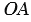 и
и 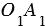 секущей
секущей 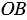 . Аналогично,
. Аналогично, 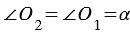 , следовательно,
, следовательно, 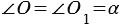 , т.е. угол между векторами не зависит от выбора точки, от которой откладываются векторы. В случае если векторы
, т.е. угол между векторами не зависит от выбора точки, от которой откладываются векторы. В случае если векторы 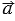 и
и 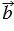 являются сонаправленными (частный случай: один из векторов или оба нулевые), тогда угол между данными векторами будем считать равным 00.
являются сонаправленными (частный случай: один из векторов или оба нулевые), тогда угол между данными векторами будем считать равным 00.
Угол между векторами 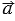 и
и 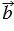 обозначается так:
обозначается так: 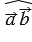 .
.
Для примера рассмотрим следующий рисунок:
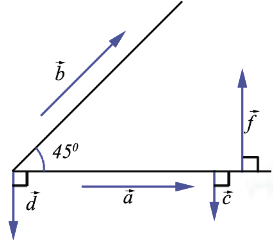
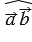 = 450,
= 450, 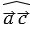 = 900,
= 900, 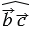 = 1350,
= 1350, 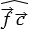 = 1800. Если угол между двумя векторами равен 900, то они называются перпендикулярными, т.е
= 1800. Если угол между двумя векторами равен 900, то они называются перпендикулярными, т.е 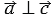 ,
, 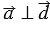 ,
, 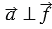 .
.
Советуем посмотреть:
Синус, косинус, тангенс, котангенс
Основное тригонометрическое тождество. Формулы приведения.
Формулы для вычисления координат точки
Теорема о площади треугольника
Скалярное произведение векторов
Скалярное произведение в координатах
Свойства скалярного произведения векторов
Соотношения между сторонами и углами треугольника. Скалярное произведение векторов
Правило встречается в следующих упражнениях:
7 класс
Задание 1039, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1041, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1068, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1069, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 14, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 15, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 17, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 19, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник