Равенство векторов
Определение
| Ненулевые векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых; нулевой вектор считается коллинеарным любому вектору. |
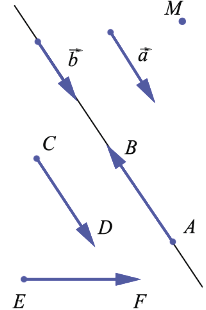
На данном рисунке векторы 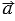 ,
, 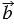 ,
, 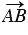 ,
, 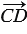 ,
, 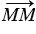 коллинеарны, а векторы
коллинеарны, а векторы 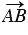 и
и 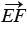 , а также
, а также 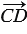 и
и 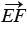 не коллинеарны.
не коллинеарны.
Два коллинеарных ненулевых вектора 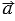 и
и 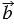 могут быть направлены либо одинаково, либо противоположно. В первом случае векторы
могут быть направлены либо одинаково, либо противоположно. В первом случае векторы 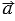 и
и 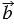 называются сонаправленными (обозначается
называются сонаправленными (обозначается 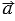
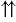
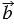 ), а во втором - противоположно направленными (обозначается
), а во втором - противоположно направленными (обозначается 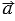
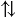
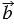 ). Любое направление можно считать направлением нулевого вектора, так как его начало совпадает с его концом. Поэтому нулевой вектор сонаправлен с любым вектором.
). Любое направление можно считать направлением нулевого вектора, так как его начало совпадает с его концом. Поэтому нулевой вектор сонаправлен с любым вектором.
На рисунке 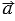
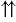
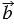 ,
, 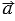
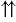
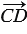 ,
, 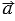
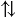
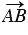 ,
, 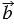
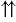
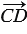 ,
, 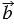
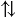
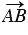 ,
, 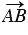
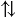
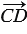 и
и 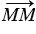
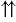
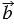 ,
, 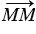
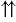
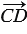 и т.д.
и т.д.
Ненулевые коллинеарные векторы обладают следующими свойствами:
- Если
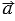
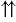
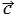 ,
, 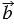
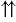
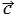 , то
, то 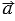
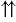
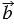 (
(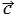
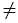
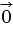 ).
). - Если
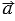
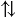
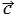 ,
, 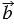
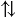
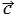 , то
, то 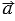
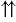
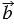 .
. - Если
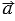
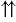
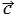 ,
, 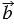
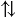
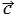 , то
, то 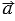
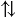
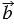 .
.
Определение
| Векторы называются равными, если они сонаправлены и их длины равны |
Таким образом, векторы 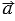 и
и 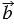 равны, если
равны, если 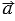
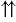
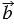 и
и 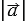 =
=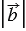 . Равенство векторов
. Равенство векторов 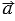 и
и 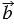 обозначается так:
обозначается так: 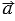 =
=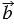 .
.
Советуем посмотреть:
Откладывание вектора от данной точки
Законы сложения векторов. Правило параллелограмма
Применение векторов к решению задач
Правило встречается в следующих упражнениях:
7 класс
Задание 756, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 775, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 801, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 910, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 912, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 914, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1163, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1165, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1178, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 5, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник