Теорема о площади треугольника / Соотношения между сторонами и углами треугольника. Скалярное произведение векторов / Справочник по геометрии 7-9 класс

Теорема

Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

Доказательство

Дано: 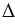АВС, ВС = 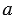, СА = 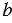, 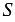- площадь 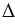АВС.

Доказать: .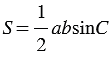

Доказательство:

Введем прямоугольную систему координат с началом в точке С так, чтобы точка В лежала на положительной полуоси 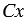, а точка А имела положительную ординату.

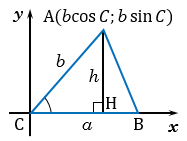
Площадь треугольника АВС можно вычислить по формул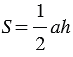е , где 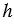- высота треугольника, но 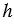равна ординате точки А, т.е. 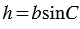(смотри формулы для вычисления координат точки). Следовательно, 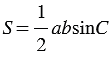. Теорема доказана.

Советуем посмотреть:

Синус, косинус, тангенс, котангенс

Основное тригонометрическое тождество. Формулы приведения.

Формулы для вычисления координат точки

Угловой коэффициент прямой

Теорема синусов

Теорема косинусов

Решение треугольников

Измерительные работы

Угол между векторами

Скалярное произведение векторов

Скалярное произведение в координатах

Свойства скалярного произведения векторов

Соотношения между сторонами и углами треугольника. Скалярное произведение векторов

Правило встречается в следующих упражнениях:

7 класс

Задание 1023, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1024, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1058, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1070, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1071, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1238, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1241, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1270, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1274, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1277, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник