Понятие вектора
Векторными величинами (векторами) называются физические величины, которые характеризуются не только своим числовым значением, но и направлением в пространстве. Например сила, перемещение материальной точки, скорость.
Концы произвольного отрезка называются его граничными точками. На отрезке можно указать два направления: от одной граничной точки к другой и наоборот.
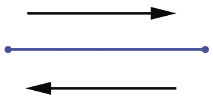
Одну граничную точку отрезка назовём началом отрезка, другую - концом отрезка, это необходимо для выбора одного из направлений. При этом будем считать, что отрезок направлен от начала к концу.
Определение
| Отрезок, для которого указано, какая из его граничных точек считается началом, а какая - концом, называется направленным отрезком или вектором |
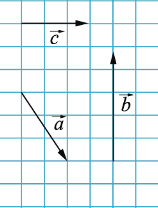
На рисунках вектор изображается отрезком со стрелкой, которая показывает направление вектора. Его обозначают двумя заглавными латинскими буквами со стрелкой над ними, например 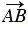 , читают вектор АВ. При этом первая буква обозначает начало вектора, вторая - конец.
, читают вектор АВ. При этом первая буква обозначает начало вектора, вторая - конец.
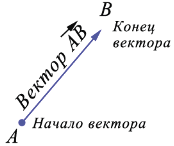
Также векторы часто обозначают одной строчной латинской буквой со стрелкой над ней: 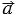 ,
, 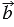 ,
, 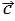 .
.
Также любая точка на плоскости является вектором. В этом случае вектор является нулевым или нуль-вектором. И его начало совпадает с его концом.
Изобразим векторы 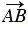 ,
, 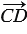 ,
, 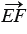 и
и 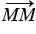 :
:
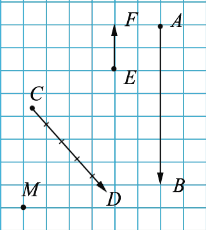
Точки А, С, Е, М - начала этих векторов, а B, D, F, М - их концы. То есть если точка, которая изображает нулевой вектор, обозначена буквой М, то нулевой вектор обозначается так: 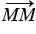 . Также его можно обозначить символом
. Также его можно обозначить символом 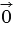 . Мы изобразили ненулевые векторы
. Мы изобразили ненулевые векторы 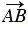 ,
, 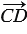 ,
, 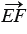 и нулевой вектор
и нулевой вектор 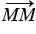 .
.
Длиной или модулем ненулевого вектора 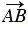 называется длина отрезка АВ. Длина вектора
называется длина отрезка АВ. Длина вектора 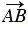 (вектора
(вектора 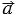 ) и обозначается так:
) и обозначается так: 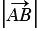 (
(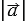 ). Длина нулевого вектора считается равной нулю:
). Длина нулевого вектора считается равной нулю: 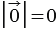 .
.
Длины изображенных выше векторов таковы: 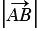 =7,
=7, 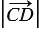 =5,
=5, 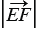 =2,
=2, 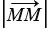 =0,
=0, 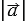 =
=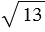 ,
, 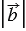 =4,5,
=4,5, 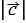 =3.
=3.
Советуем посмотреть:
Откладывание вектора от данной точки
Законы сложения векторов. Правило параллелограмма
Применение векторов к решению задач
Правило встречается в следующих упражнениях:
7 класс
Задание 753, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 790, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 802, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 808, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 928, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 11, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 3, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 9, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 20, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 21, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник