Формулы для вычисления координат точки
Введем прямоугольную систему координат 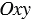 . Возьмем произвольную точку
. Возьмем произвольную точку 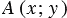 :
:
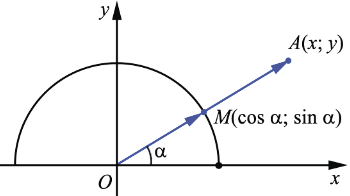
Выразим координаты данной точки через длину отрезка ОА и угол 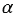 между лучом ОА и положительной полуосью абсцисс. Пусть М - точка пересечения луча ОА и единичной полуокружности. Мы знаем, что координаты точки М соответственно равны
между лучом ОА и положительной полуосью абсцисс. Пусть М - точка пересечения луча ОА и единичной полуокружности. Мы знаем, что координаты точки М соответственно равны 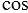
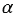 и
и 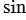
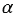 . Координаты точки М равны соответствующим координатам ее радиус-вектора, поэтому
. Координаты точки М равны соответствующим координатам ее радиус-вектора, поэтому 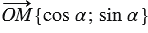 . Аналогично из того, что точка А имеет координаты
. Аналогично из того, что точка А имеет координаты 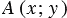 , следует, что
, следует, что 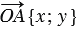 . Но
. Но 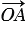 =
= 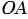

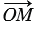 , значит:
, значит:
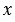 = = 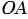  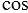 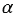 , , 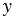 = = 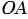  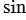 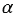 . . |
Советуем посмотреть:
Синус, косинус, тангенс, котангенс
Основное тригонометрическое тождество. Формулы приведения.
Теорема о площади треугольника
Скалярное произведение векторов
Скалярное произведение в координатах
Свойства скалярного произведения векторов
Соотношения между сторонами и углами треугольника. Скалярное произведение векторов
Правило встречается в следующих упражнениях:
7 класс
Задание 1018, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 8, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 10, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник