Скалярное произведение в координатах
Теорема
|
В прямоугольной системе координат скалярное произведение векторов
|
Доказательство
Дано: 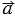
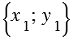 ,
, 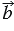
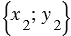
Доказать: 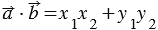
Доказательство:
Каждая координата вектора равна разности соответствующих координат его конца и начала, поэтому если хотя бы один из векторов нулевой, то справедливость равенства очевидна, так как координаты нулевого вектора равны нулю.
Рассмотрим ненулевые векторы 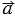 и
и 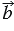 . Отложим от произвольной точки О векторы
. Отложим от произвольной точки О векторы 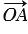 =
= 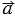 и
и 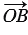 =
= 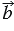 :
:
1 случай: векторы 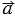 и
и 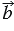 не коллинеарны:
не коллинеарны:
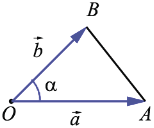
Тогда по теореме косинусов получаем
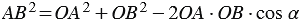 . (2)
. (2)
2 случай: векторы 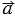 и
и 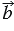 сонаправленные:
сонаправленные:

Тогда 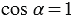 и получаем, что
и получаем, что
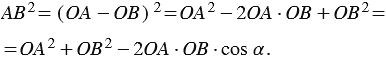
3 случай: векторы 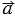 и
и 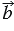 противоположно направленные:
противоположно направленные:
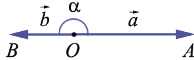
Тогда 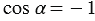 и получаем, что
и получаем, что
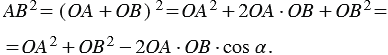
Итак, мы получили, что равенство (2) верно для любых двух ненулевых векторов 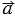 и
и 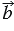 .
.
Так как 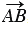 =
= 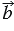 -
- 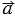 ,
, 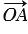 =
= 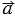 ,
, 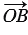 =
= 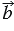 , то равенство (2) можно записать следующим образом:
, то равенство (2) можно записать следующим образом:
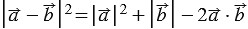
Следовательно,
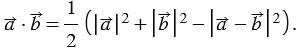
Вектора имеют следующие координаты 
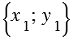 ,
, 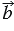
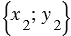 и (
и (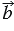 -
- 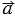 )
)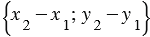 , при этом длина вектора равна квадратному корню из суммы квадратов координат данного вектора, поэтому
, при этом длина вектора равна квадратному корню из суммы квадратов координат данного вектора, поэтому
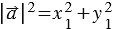 ,
, 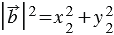
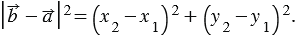
Учитывая это, получаем
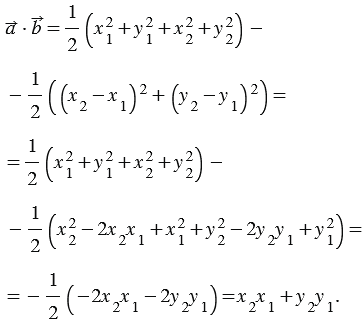
Итак, 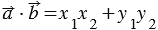 , что и требовалось доказать. Теорема доказана.
, что и требовалось доказать. Теорема доказана.
Следствие 1
Ненулевые векторы 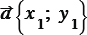 и и 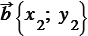 перпендикулярны тогда и только тогда, когда перпендикулярны тогда и только тогда, когда 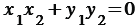 . . |
Следствие 2
|
Косинус угла
|
Советуем посмотреть:
Синус, косинус, тангенс, котангенс
Основное тригонометрическое тождество. Формулы приведения.
Формулы для вычисления координат точки
Теорема о площади треугольника
Скалярное произведение векторов
Свойства скалярного произведения векторов
Соотношения между сторонами и углами треугольника. Скалярное произведение векторов
Правило встречается в следующих упражнениях:
7 класс
Задание 1044, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1073, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 18, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 20, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
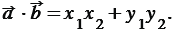 (1)
(1)
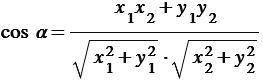 .
.