Скалярное произведение векторов

Определение

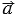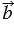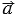
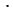
Пусть нам даны векторы и , тогда их скалярное произведение будет обозначаться так: 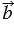или .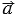

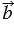Из определения мы можем записать:

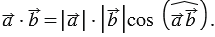             (1)

Утверждение:

Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.

Доказательство:

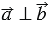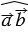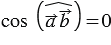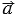
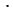
Пусть , т.е. = 90⁰, тогда , а, значит, 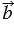= 0.

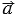Пусть и 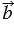ненулевые, при этом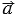 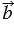= 0, тогда из равенства (1) получаем, что 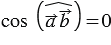, а, значит, 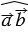= 90⁰, т.е. 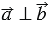. Следовательно, утверждение верно.

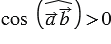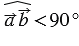Так как при ( при 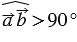) тогда из формулы (1) следует, что скалярное произведение ненулевых векторов 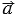и 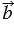положительно (отрицательно) тогда и только тогда, когда ().

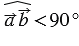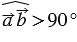Пусть векторы 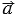и 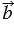будут являться сонаправленными, тогда угол между ними будет равен 0⁰ и 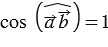, тогда из формулы (1) получим 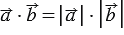. Частным случаем является произведение вектора на себя, т.е.

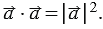
Скалярное произведение 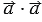называется скалярным квадратом вектора 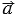и обозначается 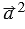. Скалярный квадрат вектора равен квадрату его длины.