Свойства скалярного произведения векторов
Свойства скалярного произведения векторов:
|
Для любых векторов 10. 20. 30. 40. |
Из формулы 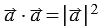 следует утверждение 10, а из определения скалярного произведения следует утверждение 20.
следует утверждение 10, а из определения скалярного произведения следует утверждение 20.
Докажем утверждение 30:
Введем прямоугольную систему координат. Пусть векторы в данной системе координат имеют следующие координаты: 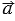
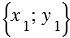 ,
, 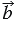
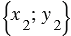 ,
, 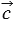
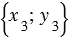 . Используем формулу, выражающую скалярное произведение векторов в прямоугольной системе координат:
. Используем формулу, выражающую скалярное произведение векторов в прямоугольной системе координат:
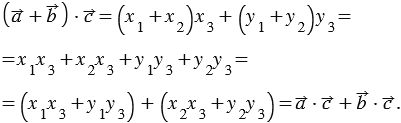
Докажем утверждение 40:
Введем прямоугольную систему координат. Пусть векторы в данной системе координат имеют следующие координаты: 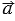
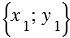 ,
, 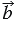
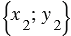 . Тогда вектор
. Тогда вектор 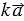 имеет координаты
имеет координаты 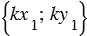 , а, значит, используя формулу, выражающую скалярное произведение векторов в прямоугольной системе координат, получим:
, а, значит, используя формулу, выражающую скалярное произведение векторов в прямоугольной системе координат, получим:
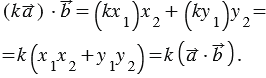
Замечание
Распределительный закон имеет место для любого числа слагаемых.
Советуем посмотреть:
Синус, косинус, тангенс, котангенс
Основное тригонометрическое тождество. Формулы приведения.
Формулы для вычисления координат точки
Теорема о площади треугольника
Скалярное произведение векторов
Скалярное произведение в координатах
Соотношения между сторонами и углами треугольника. Скалярное произведение векторов
Правило встречается в следующих упражнениях:
7 класс
Задание 1046, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1051, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 21, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
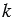 справедливы соотношения:
справедливы соотношения: 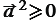 , причём
, причём 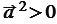 при
при 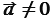 .
.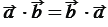 (переместительный закон).
(переместительный закон).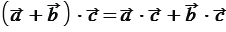 (распределительный закон).
(распределительный закон).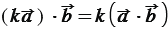 (сочетательный закон).
(сочетательный закон).