Теорема косинусов / Соотношения между сторонами и углами треугольника. Скалярное произведение векторов / Справочник по геометрии 7-9 класс

Теорема косинусов

Теорема

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон, умноженное на косинус угла между ними.

Доказательство

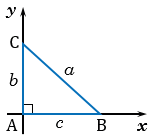
Дано: 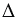АВС, АВ = 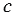, ВС = 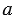, АС = .

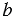Доказать: 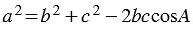. (1)

Доказательство:

Введем прямоугольную систему координат с началом в точке А так, чтобы точка В лежала на положительной полуоси 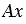, а точка С имела положительную ординату.

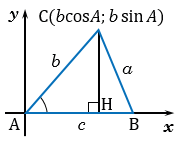
Точка В имеет координаты (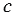; 0).

Точка С имеет координаты (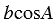; 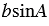) (смотри формулы для вычисления координат точки).

По формуле расстояния между двумя точками получаем:

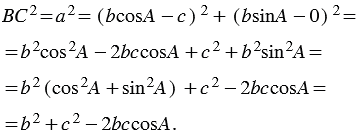
(При выполнении вычислений мы использовали основное тригонометрическое тождество: ).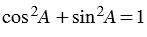

Теорема доказана.

Теорему косинусов еще называют обобщенной теоремой Пифагора. Такое название объясняется тем, что в теореме косинусов содержится как частный случай теорема Пифагора. В самом деле, если в 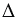АВС угол А прямой, то 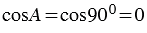и по формуле (1) получаем 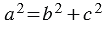, т.е. квадрат гипотенузы равен сумме квадратов катетов (теорема Пифагора).

Теорема косинусов

Доказательство

Советуем посмотреть:

Правило встречается в следующих упражнениях: