Измерительные работы
Измерение высоты предмета
Пусть нам нужно определить высоту АН какого-то предмета, например, высоту дерева (смотри рисунок ниже).
На определенном расстоянии 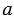 от основания Н предмета (дерева) отметим точку В и измерим угол АВН:
от основания Н предмета (дерева) отметим точку В и измерим угол АВН:  АВН =
АВН = 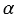 .
.
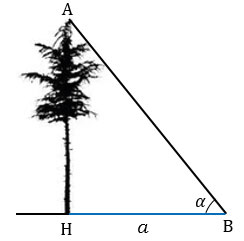
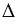 АВН - прямоугольный, следовательно, мы можем найти тангенс угла
АВН - прямоугольный, следовательно, мы можем найти тангенс угла 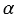 :
: 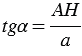 , откуда высота предмета (дерева)
, откуда высота предмета (дерева) 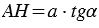 .
.
Если основание предмета недоступно, то на прямой, проходящей через основание Н предмета (дерева) отметим две точки В и С на определенном расстоянии 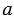 друг от друга и измерим углы АВН и АСВ:
друг от друга и измерим углы АВН и АСВ:  АВН =
АВН = 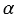 и
и  АСВ =
АСВ = 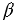 .
.
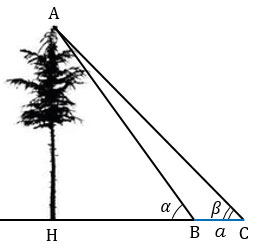
 АВН - внешний угол
АВН - внешний угол 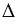 АВС, поэтому
АВС, поэтому  ВАС +
ВАС +  АСВ =
АСВ =  АВН, откуда
АВН, откуда  ВАС =
ВАС =  АВН -
АВН -  АСВ =
АСВ = 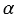 -
- 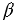 .
.
Итак, в 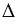 АВС известны три элемента: ВС =
АВС известны три элемента: ВС = 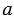 ,
,  АСВ =
АСВ = 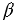 ,
,  ВАС =
ВАС = 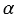 -
- 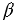 , следовательно, мы можем решить треугольник
, следовательно, мы можем решить треугольник 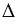 АВС, в частности найти сторону АВ.
АВС, в частности найти сторону АВ.
По теореме синусов 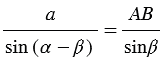 , откуда
, откуда 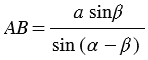 .
.
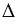 АВН - прямоугольный, следовательно, мы можем найти синус угла
АВН - прямоугольный, следовательно, мы можем найти синус угла 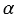 :
: 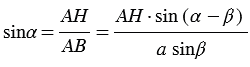 , откуда высота предмета (дерева)
, откуда высота предмета (дерева) 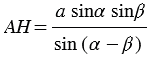 .
.
Измерение расстояния до недоступной точки
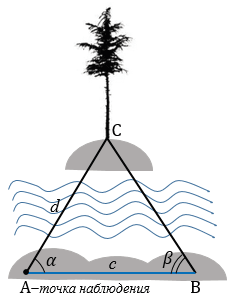
Пусть нам надо найти расстояние 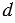 от пункта А до недоступного пункта С (см. рисунок ниже).
от пункта А до недоступного пункта С (см. рисунок ниже).
На местности выберем точку В и измерим длину 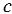 отрезка АВ. Затем измерим, например с помощью астролябии, углы А и В:
отрезка АВ. Затем измерим, например с помощью астролябии, углы А и В:  А =
А = 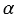 и
и  В =
В = 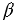 .
.
В 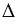 АВС известны три элемента: АВ =
АВС известны три элемента: АВ = 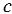 ,
,  А =
А = 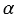 ,
,  В =
В = 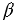 , следовательно, мы можем решить треугольник
, следовательно, мы можем решить треугольник 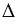 АВС, в частности найти расстояние
АВС, в частности найти расстояние 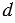 = АС.
= АС.
По теореме о сумме углов треугольника:  А +
А +  В +
В +  С = 1800. Следовательно,
С = 1800. Следовательно,  С = 1800 - (
С = 1800 - ( А +
А +  В) или
В) или  С = 1800 -
С = 1800 -  А -
А -  В = 1800 -
В = 1800 - 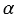 -
- 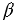 .
.
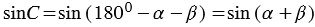 (смотри формулы приведения).
(смотри формулы приведения).
По теореме синусов: 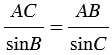 или
или 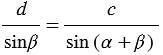 , откуда
, откуда 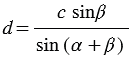 .
.
Рассмотренные выше задачи также можно решить с помощью признаков подобия треугольников.
Советуем посмотреть:
Синус, косинус, тангенс, котангенс
Основное тригонометрическое тождество. Формулы приведения.
Формулы для вычисления координат точки
Теорема о площади треугольника
Скалярное произведение векторов
Скалярное произведение в координатах
Свойства скалярного произведения векторов
Соотношения между сторонами и углами треугольника. Скалярное произведение векторов
Правило встречается в следующих упражнениях:
7 класс
Задание 1036, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1037, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1038, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 12, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 13, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник