Решение треугольников
Решение треугольника - это нахождение всех его шести элементов (т.е. трех сторон и трех углов) по каким-нибудь трем данным элементам, определяющим треугольник.
Введем обозначения для сторон 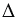 АВС: АВ =
АВС: АВ = 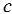 , ВС =
, ВС = 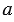 , СА =
, СА = 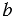 .
.
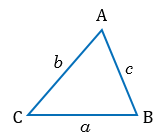
Далее рассмотрим задачи на решение треугольников с использованием данных обозначений.
Задача 1
| Решение треугольника по двум сторонам и углу между ними. |
Дано: 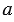 ,
, 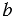 ,
,  С.
С.
Найти: 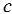 ,
,  А,
А,  В.
В.
Решение:
1. По теореме косинусов: 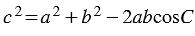 , откуда
, откуда 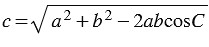 .
.
2. По теореме косинусов: 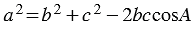 , откуда
, откуда 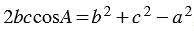 , следовательно,
, следовательно, 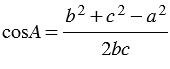 . Далее угол А находим с помощью микрокалькулятора или по таблице.
. Далее угол А находим с помощью микрокалькулятора или по таблице.
3. По теореме о сумме углов треугольника:  А +
А +  В +
В +  С = 1800. Следовательно,
С = 1800. Следовательно,  В = 1800 - (
В = 1800 - ( А +
А +  С) или
С) или  В = 1800 -
В = 1800 -  А -
А -  С.
С.
Задача 2
| Решение треугольника по стороне и прилежащим к ней углам. |
Дано: 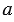 ,
,  В,
В,  С.
С.
Найти:  А,
А, 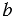 ,
, 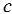 .
.
Решение:
1. По теореме о сумме углов треугольника:  А +
А +  В +
В +  С = 1800. Следовательно,
С = 1800. Следовательно,  А = 1800 - (
А = 1800 - ( В +
В +  С) или
С) или  А = 1800 -
А = 1800 -  В -
В -  С.
С.
2. По теореме синусов: 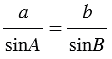 , откуда
, откуда 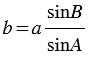 .
.
3. По теореме синусов: 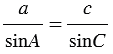 , откуда
, откуда 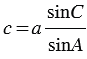 .
.
Задача 3
| Решение треугольника по трем сторонам. |
Дано: 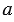 ,
, 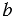 ,
, 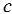 .
.
Найти:  А,
А,  В,
В,  С.
С.
Решение:
1. По теореме косинусов: 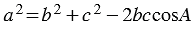 , откуда
, откуда 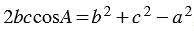 , следовательно,
, следовательно, 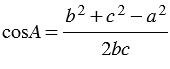 . Далее угол А находим с помощью микрокалькулятора или по таблице.
. Далее угол А находим с помощью микрокалькулятора или по таблице.
2. По теореме косинусов: 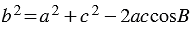 , откуда
, откуда 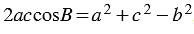 , следовательно,
, следовательно, 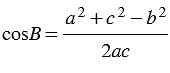 . Далее угол В находим с помощью микрокалькулятора или по таблице.
. Далее угол В находим с помощью микрокалькулятора или по таблице.
3. По теореме о сумме углов треугольника:  А +
А +  В +
В +  С = 1800. Следовательно,
С = 1800. Следовательно,  С = 1800 - (
С = 1800 - ( А +
А +  В) или
В) или  С = 1800 -
С = 1800 -  А -
А -  В.
В.
Пример
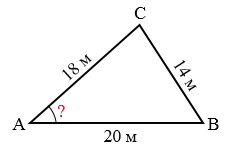
Стороны АВ, ВС и АС треугольника АВС соответственно равны 20 м, 14 м и 18 м. Определите значение угла А.
Решение:
По условию задачи 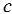 = АВ = 20 м,
= АВ = 20 м, 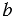 = АС = 18 м,
= АС = 18 м, 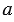 = ВС = 14 м.
= ВС = 14 м.
Следовательно, мы можем решить данный треугольник по трем сторонам (см. задачу 3), значит, найти угол А.
По теореме косинусов: 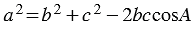 , откуда
, откуда 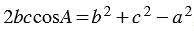 , следовательно,
, следовательно,
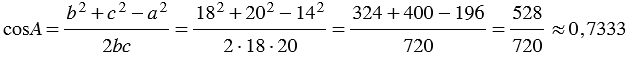 .
.
По таблице Брадиса находим угол А: 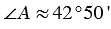 .
.
Советуем посмотреть:
Синус, косинус, тангенс, котангенс
Основное тригонометрическое тождество. Формулы приведения.
Формулы для вычисления координат точки
Теорема о площади треугольника
Скалярное произведение векторов
Скалярное произведение в координатах
Свойства скалярного произведения векторов
Соотношения между сторонами и углами треугольника. Скалярное произведение векторов
Правило встречается в следующих упражнениях:
7 класс
Задание 1025, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1060, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1061, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 11, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 12, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 13, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник