Синус, косинус, тангенс, котангенс

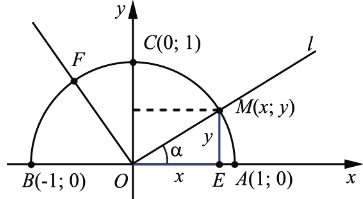
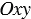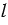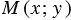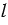Введем прямоугольную систему координат . В верхней полуплоскости координатной плоскости рассмотрим полуокружность радиуса 1 с центром в начале координат, её называют единичной полуокружностью. Из точки О(0; 0) проведем луч и отметим точку , в которой данный луч пересекает единичную полуокружность. Пусть -  угол между лучом и положительной полуосью абсцисс (при совпадении данного луча с положительной полуосью абсцисс будем считать, что = 0⁰):

Пусть 90⁰, тогда из прямоугольного треугольника ЕОМ получаем: 

, .

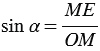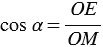Учитывая, что ОМ = 1, МЕ = 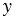, ОЕ = 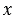, получим:

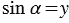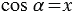, .                 (1)

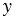То есть синус острого угла равен ординате точки М, а косинус - абсциссе 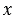 точки М.

Формулы (1) справедливы и в том случае, если угол прямой, тупой и развёрнутый (на рисунке выше 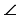АОС, 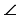АОF и 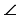АОВ). Значит, для любого угла из промежутка 0⁰ 180⁰ синусом угла называется ордината 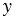точки М, а косинусом угла - абсцисса 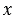точки М.

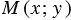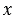
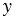
Если - произвольная точка единичной полуокружности, то -1 1 и 0 1, тогда для любого угла из промежутка 0⁰ 180⁰ имеем:

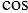
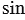
-1 1 и 0 1.

Лучи ОА, ОС и ОВ соответствуют углам, которые равны 0⁰, 90⁰ и 180⁰ соответственно. Точки А, С и В имеют координаты А(1; 0), С(0; 1) и В(-1; 0), поэтому

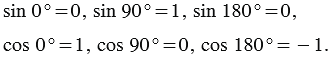(2)

Тангенсом угла ( 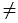90⁰) называют отношение 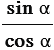, т.е.

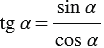      (3)

Так как 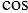90⁰ = 0, то знаменатель в формуле (3) обращается в нуль, значит,  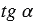при = 90⁰ не определён.

Котангенсом угла  (0⁰ 180⁰) называется отношение 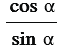. Котангенс угла обозначается символом 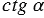. Таким  образом,

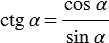.      (4)

Так как 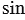0⁰ = 0 и  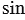180⁰ = 0, то знаменатель в формуле (4) обращается в нуль, значит,  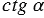при = 0⁰  и = 180⁰ не определён.