Основное тригонометрическое тождество. Формулы приведения. / Соотношения между сторонами и углами треугольника. Скалярное произведение векторов / Справочник по геометрии 7-9 класс

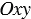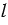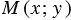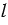Введем прямоугольную систему координат . Начертим единичную полуокружность АСВ в верхней полуплоскости координатной плоскости. Из точки О(0; 0) проведем луч и отметим точку , в который данный луч пересекает полуокружность АСВ. Пусть - угол между лучом и положительной полуосью абсцисс:

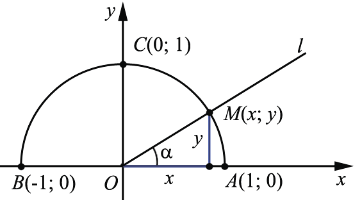
Данная полуокружность является дугой окружности, которая имеет уравнение 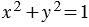(1). Нам известно, что 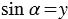и 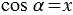, поэтому из уравнения (1) получим равенство

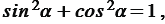(2)

которое выполняется для любого 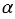из промежутка 0⁰ 180⁰. Равенство (2) - это основное тригонометрическое тождество.

Формулы приведения:

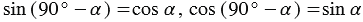
при 0⁰ 90⁰

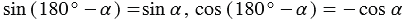
при 0⁰ 180⁰.

Советуем посмотреть:

Синус, косинус, тангенс, котангенс

Формулы для вычисления координат точки

Угловой коэффициент прямой

Теорема о площади треугольника

Теорема синусов

Теорема косинусов

Решение треугольников

Измерительные работы

Угол между векторами

Скалярное произведение векторов

Скалярное произведение в координатах

Свойства скалярного произведения векторов

Соотношения между сторонами и углами треугольника. Скалярное произведение векторов

Правило встречается в следующих упражнениях:

7 класс

Задание 1013, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1016, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1018, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1023, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1030, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1233, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1270, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1273, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1276, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 13, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник