Измерительные работы на местности

Свойства подобных треугольников могут быть использованы при проведении различных измерительных работ на местности.

Определение высоты предмета

Пусть нам нужно определить высоту телеграфного столба А₁С₁.

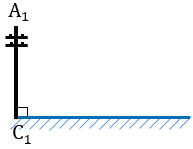
Для этого на некотором расстоянии от столба ставим шест АС с вращающейся планкой и направляем планку на верхнюю точку столба А₁.

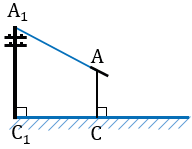
Далее отмечаем на поверхности земли точку В, в которой прямая А₁А пересекается с поверхностью земли.

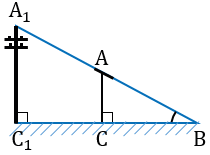
В А₁С₁В и АСВ: С₁ =С = 90⁰, В - общий, следовательно, А₁С₁ВАСВ (по 1 признаку подобия треугольников), поэтому сходственные стороны треугольников А₁С₁В и АСВ пропорциональны: 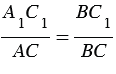, откуда .

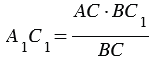Измерив расстояния ВС₁ и ВС, зная длину шеста АС, по полученной формуле вычисляем высоту А₁С₁ телеграфного столба. Пусть, например, ВС₁ = 6,3 м, ВС = 2,1 м, АС = 1,7 м, тогда: 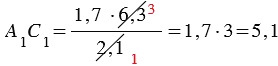м.

Определение расстояния до недоступной точки

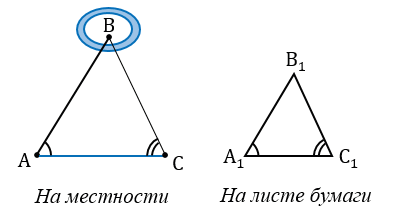
Пусть, нам нужно найти расстояние от пункта А до недоступного пункта В.

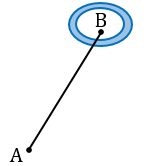
Для этого на местности выбираем точку С, провешиваем отрезок АС и измеряем его.

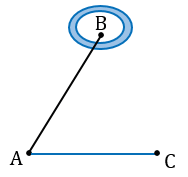
Затем с помощью астролябии измеряем углы А и С.

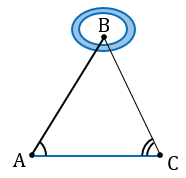
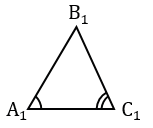
На листе бумаги строим какой-нибудь треугольник А₁В₁С₁, у которого А₁ =А и С₁ =С. Для того, чтобы построить на листе бумаги углы А₁ и С₁ используем транспортир.

А₁В₁С₁АВС (по 1 признаку подобия треугольников). Из подобия треугольников А₁В₁С₁ и АВС следует, что сходственные стороны данных треугольников пропорциональны: 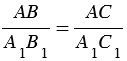, откуда .

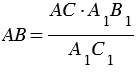Измерив при помощи линейки длину отрезков А₁В₁ и А₁С₁, зная расстояние АС, по полученной формуле вычисляем расстояние АВ.

Чтобы сделать вычисления проще, А₁В₁С₁ удобно построить так, чтобы А₁С₁ : АС = 1 : 1000. Например, если АС = 120 м = 120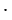1000 мм (1 м = 1000 мм), то расстояние А₁С₁ берем равным 120 мм. Тогда 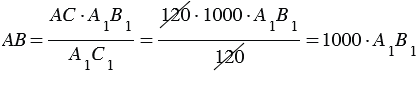, поэтому измерив расстояние А₁В₁ в миллиметрах, мы сразу получим расстояние АВ в метрах, т.к. в 1 м = 1000 мм.

Пример:

Пусть АС = 130 м, А = 73⁰, С = 58⁰. На бумаге строим треугольник А₁В₁С₁, так, чтобы А₁ = 73⁰, С₁ = 58⁰, А₁С₁ = 130 мм.

Измеряем с помощью линейки отрезок А₁В₁. Он равен 153 мм, поэтому искомое расстояние АВ = 153 м.