Задание 360 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№360 учебника 2013-2022 (стр. 96):
Постройте треугольник по периметру, одному из углов и высоте, проведенной из вершины другого угла.
№360 учебника 2023-2024 (стр. 104):
Подсказка
№360 учебника 2013-2022 (стр. 96):
Вспомните:
- Что такое периметр треугольника.
- Что такое высота треугольника.
- Как построить отрезок, равный данному.
- Как построить перпендикулярные прямые.
№360 учебника 2023-2024 (стр. 104):
Вспомните:
- Какой треугольник называют прямоугольным.
- Что называют высотой треугольника..
- Как построить середину отрезка.
- Что называют окружностью.
- Какие прямые называют параллельными.
- Как построить перпендикулярные прямые.
Ответ
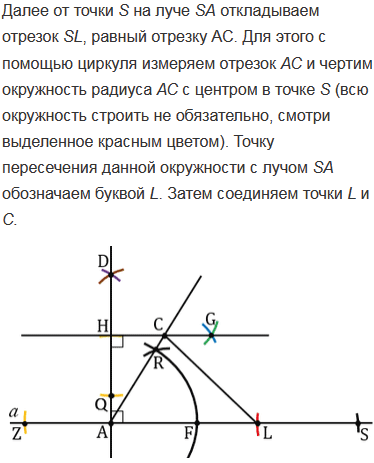
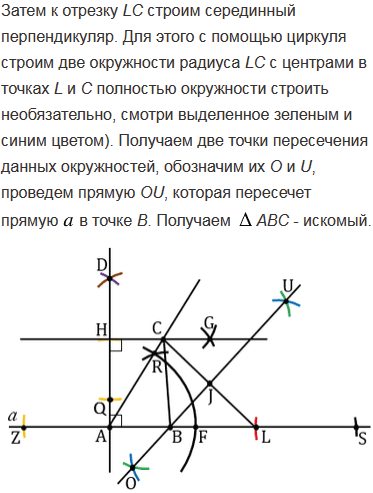
№360 учебника 2013-2022 (стр. 96):


№360 учебника 2023-2024 (стр. 104):
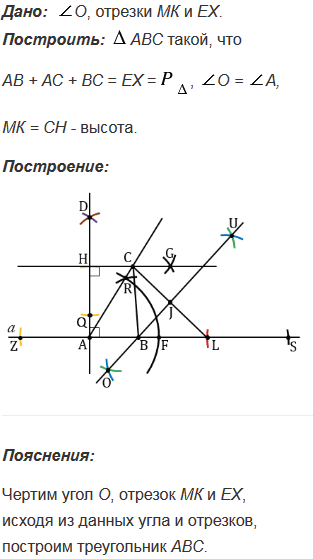
Дано: отрезки РЕ и МN.
Построить: прямоугольный треугольник так, что РЕ - гипотенуза, МN - высота к гипотенузе.
Решение:
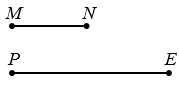
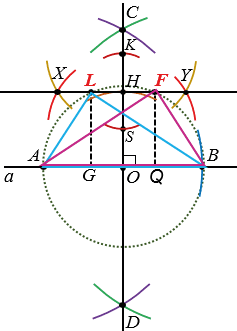
АВ = РЕ, LG = FQ = MN.
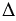 АLB и
АLB и 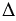 АFB - искомые треугольники.
АFB - искомые треугольники.
Пояснения:
Пусть нам даны отрезки РЕ и MN, построим прямоугольный треугольник, у которого гипотенуза равна РЕ, а высота - MN.
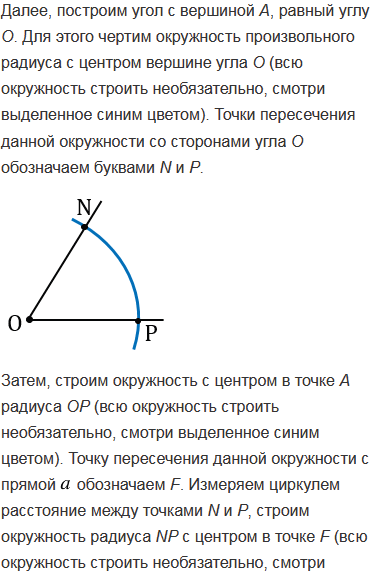
Сначала построим отрезок АВ, равный отрезку РЕ. Для этого с помощью линейки чертим прямую 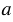 , ставим на ней точку А и с помощью циркуля чертим окружность радиуса РЕ с центром в точке А (полностью окружность можно не строить). Точка пересечения этой окружности с прямой
, ставим на ней точку А и с помощью циркуля чертим окружность радиуса РЕ с центром в точке А (полностью окружность можно не строить). Точка пересечения этой окружности с прямой 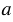 и будет точка В.
и будет точка В.
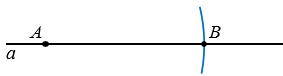
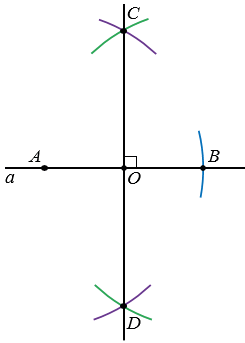
Далее построим середину отрезка АВ - точку О. Для этого строим с помощью циркуля две окружности радиуса АВ с центрами в точках А и В (полностью окружности можно не строить). Получаем две точки пересечения данных окружностей. Обозначим их С и D. Проведем с помощью линейки через точки C и D прямую CD, которая пересечет АВ в точке О - середине отрезка АВ.
Причем, СD - серединный перпендикуляр к отрезку АВ, т.к. каждая точка прямой СD равноудалена от его концов А и В.
Теперь проведем окружность с центром О радиуса МN (полностью окружность строить необязательно). Она пересечет луч ОС в точке H.
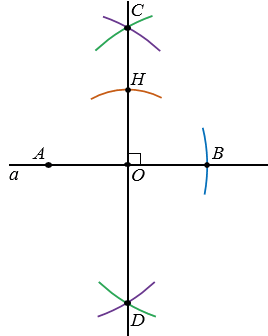
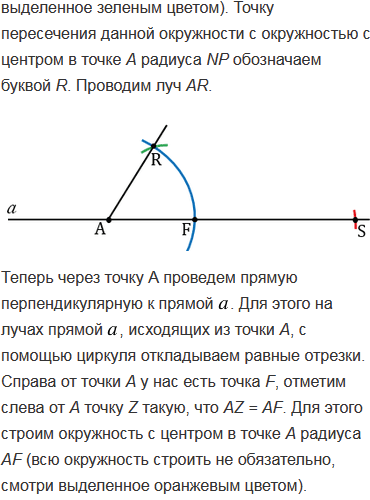
Далее через точку Н проведем прямую, параллельную прямой 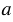 . На лучах, исходящих из точки Н, с помощью циркуля откладываем равные отрезки НК и НS (НK = HS). Для этого строим окружность с центром в точке Н, при этом всю окружность строить не обязательно, достаточно сделать пометки по разные стороны от точки Н. Затем строим две окружности с центрами в точках K и S радиуса KS (полностью окружности строить необязательно). Данные окружности пересекутся в двух точках, обозначим их X и Y. Проведем с помощью линейки через точки Х и Y прямую. Прямая ХУ будет параллельна прямой
. На лучах, исходящих из точки Н, с помощью циркуля откладываем равные отрезки НК и НS (НK = HS). Для этого строим окружность с центром в точке Н, при этом всю окружность строить не обязательно, достаточно сделать пометки по разные стороны от точки Н. Затем строим две окружности с центрами в точках K и S радиуса KS (полностью окружности строить необязательно). Данные окружности пересекутся в двух точках, обозначим их X и Y. Проведем с помощью линейки через точки Х и Y прямую. Прямая ХУ будет параллельна прямой  .
.
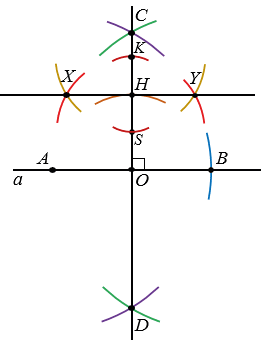
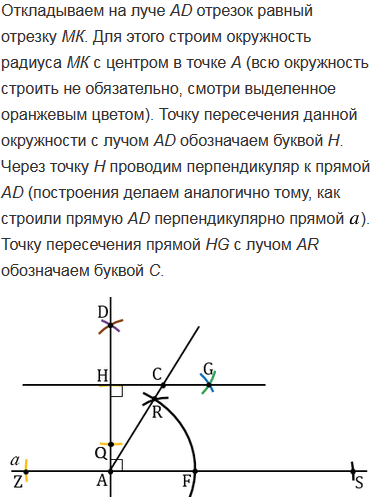
Теперь проводим окружность с центром О радиуса ОА. Данная окружность пересечет прямую ХУ в дух точках L и F.
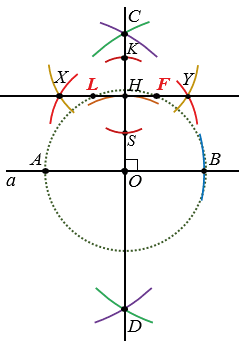
Мы получили два прямоугольных треугольника, у которых гипотенуза АВ равна отрезку РЕ, а высоты LG и FQ равны отрезку МN, - это треугольники АLB и АFB.

Вернуться к содержанию учебника