Задание 2.437 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№2.437 учебника 2023-2024 (стр. 102):
В День леса два отряда высадили саженцы 780 сосен, причем первый отряд высадил 95% числа саженцев, высаженных вторым отрядом. Сколько сотен посадил каждый отряд?
№2.437 учебника 2021-2022 (стр. 97):
Запишите наибольшее и наименьшее значения выражения 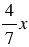 , если
, если  .
.
Подсказка
№2.437 учебника 2023-2024 (стр. 102):
Вспомните:
- Проценты.
- Что называют уравнением, его корни.
- Десятичные дроби.
- Деление десятичных дробей.
- Сложение десятичных дробей.
- Распределительное свойство умножения.
№2.437 учебника 2021-2022 (стр. 97):
Вспомните:
- Числовые и буквенные выражения.
- Умножение обыкновенных дробей.
- Сравнение дробей с разными знаменателями.
- Приведение дробей к общему знаменателю.
- Сравнение дробей с одинаковыми знаменателями.
- Основное свойство дроби (сокращение дробей).
Ответ
№2.437 учебника 2023-2024 (стр. 102):
95% = 0,95
Пусть 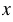 сосен высадил второй отряд, тогда первый отряд высадил 0,95
сосен высадил второй отряд, тогда первый отряд высадил 0,95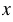 сосен. Два отряда высадили 780 сосен.
сосен. Два отряда высадили 780 сосен.
Составим уравнение:
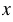 + 0,95
+ 0,95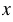 = 780
= 780
1,95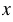 = 780
= 780
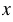 = 780 : 1,95
= 780 : 1,95
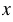 = 78 000 : 195
= 78 000 : 195
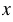 = 400 (с.) - высадил второй отряд.
= 400 (с.) - высадил второй отряд.
780 - 400 = 380 (с.) - высадил первый отряд.
Ответ: 380 сосен и 400 сосен.
Пояснения:
Решаем задачу с помощью уравнения.
Пусть 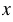 сосен высадил второй отряд. Первый отряд высадил 95% числа саженцев, высаженных вторым отрядом.
сосен высадил второй отряд. Первый отряд высадил 95% числа саженцев, высаженных вторым отрядом.
Чтобы найти несколько процентов от числа, нужно сначала перевести проценты в десятичную дробь, а затем умножить число на полученную десятичную дробь. Чтобы проценты записать в виде десятичной дроби, нужно число стоящее перед знаком % разделить на 100.
95% = 95 : 100 = 0,95.
Значит, первый отряд высадил 0,95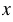 сосен.
сосен.
Два отряда вместе высадили 780 сосен. Получается, можем составить следующее уравнение:
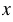 + 0,95
+ 0,95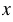 = 780.
= 780.
Упрощаем левую часть уравнения с помощью распределительного свойства умножения относительно сложения, получаем:
(1 + 0,95)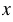 = 780,
= 780,
1,95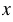 = 780.
= 780.
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель, тогда:
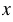 = 780 : 1,95,
= 780 : 1,95,
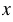 = 78 000 : 195,
= 78 000 : 195,
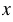 = 400.
= 400.
Учитывая обозначения, введенные выше, 400 сосен высадил второй отряд.
Вместе два отряда высадили 780 сосен, из которых 400 сосен высадил второй отряд, значит, первый отряд высадил:
780 - 400 = 380 (сосен).
№2.437 учебника 2021-2022 (стр. 97):
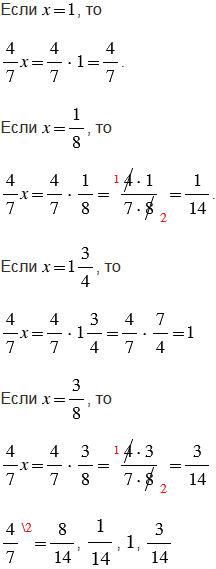

Пояснения:
Чтобы найти значение буквенного выражения при заданном значении переменной, нужно в это выражение вместо переменной подставить числа, ей соответствующие, и выполнить вычисления, учитывая следующие правила:
1) при умножении числа на единицу получается то же число;
2) произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель - произведению знаменателей. При выполнении умножения дробей, чтобы вычисления были проще, не надо перемножать сразу, лучше сделать это после сокращения. Сократить дробь - значит, разделить ее числитель и знаменатель на одно и то же число (наибольший общий делитель);
3) чтобы выполнить умножение смешанных чисел, нужно записать эти числа в виде неправильных дробей, а затем воспользоваться правилом умножения дробей. Чтобы преобразовать смешанное число в неправильную дробь, надо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в ее знаменатель записать знаменатель дробной части смешанного числа;
4) произведение взаимно обратных чисел равно единице (обратным числу 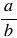 является число
является число 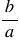 ).
).
Чтобы сравнить две дроби с разными знаменателями, надо, используя основное свойство дроби, привести данные дроби к общему знаменателю (наименьшее общее кратное знаменателей), затем применить правило сравнения дробей с одинаковыми знаменателями: из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше, и меньше та, у которой числитель меньше. При этом учитываем то, что единица больше любой правильной дроби (дроби, у которой числитель меньше знаменателя).
Вернуться к содержанию учебника