Упражнение 730 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 195

а) \(10x^2-10x+m=0\)

\(a = 10\),  \(b = -10\),  \(c = m\)

\(D=b^2 - 4ac=\)

\(=(-10)^2-4\cdot 10\cdot m=\)

\(=100-40m\)

Если \(D \ge 0\), то уравнение имеет хотя бы один корень.

\[100-40m\ge 0\]

\(-40m \ge -100\)   \(/ : (-40)\)

\(m \le \frac{100}{40}\)

\[m\le \frac{5}{2}\]

\(m \le 2,5\)

Ответ: при \(m \le 2,5\).

б) \(mx^2+4x-2=0\)

Если \(m=0\), то

\(4x-2=0\)

\(4x = 2\)

\(x = \frac24\)

\(x=0,5\)

Если \(m\ne 0\), то

\(mx^2+4x-2=0\)

\(a = m\),  \(b = 4\),  \(c = -2\)

\(D=b^2 - 4ac=\)

\(=4^2-4\cdot m\cdot (-2)=\)

\(=16+8m\)

Если \(D \ge 0\), то уравнение имеет хотя бы один корень.

\[16+8m\ge 0\]

\(8m\ge -16\)  \(/ : 8\)

\[m\ge -2\]

Ответ: при \( m\ge -2\).

в) \(3x^2+mx-5=0\)

\(a = 3\),  \(b = m\),  \(c = -5\)

\(D=b^2 - 4ac=\)

\[=m^2-4\cdot 3\cdot (-5)=\]

\[=m^2+60\]

Если \(D \ge 0\), то уравнение имеет хотя бы один корень.

\(m^2+60>0\) при любом \(m\).

Ответ: при любом \(m\).

г) \(2x^2-mx+2=0\)

\(a = 2\),  \(b = -m\),  \(c = 2\)

\(D=b^2 - 4ac=\)

\[=(-m)^2-4\cdot 2\cdot 2=\]

\[=m^2-16\]

Если \(D \ge 0\), то уравнение имеет хотя бы один корень.

\[m^2-16\ge 0\]

\((m - 4)(m + 4) \ge 0\)

\((m - 4)(m + 4) = 0\)

\(m - 4 = 0\)  или  \(m + 4 = 0\)

\(m = 4\)                 \(m = -4\)

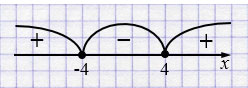
Ответ: при \(m \in (-\infty ; -4] \cup [4; +\infty )\).

Пояснения:

Квадратное уравнение

\[ax^2+bx+c=0,\]

имеет хотя бы один корень в том случае, когда дискриминант \[D=b^2-4ac\] неотрицателен, то есть \(D \ge 0\).

В каждом случае находим дискриминант уравнения и решаем неравенство, учитывая то, что дискриминант должен быть неотрицателен.