Упражнение 725 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№725 учебника 2023-2026 (стр. 194):
Из пункта \(A\) в пункт \(B\) вышел пешеход, а через \(30\) мин навстречу ему из пункта \(B\) в пункт \(A\) выехал велосипедист. Скорость велосипедиста на \(8\) км/ч больше скорости пешехода. Велосипедист через \(1{,}5\) ч после выезда встретил пешехода. С какой скоростью шёл пешеход и ехал велосипедист, если известно, что расстояние между пунктами \(A\) и \(B\) равно \(26\) км?
№725 учебника 2014-2022 (стр. 186):
На входной двери дома установлен домофон, на котором нанесены цифры \(0, 1, 2, \ldots, 8, 9\). Каждая квартира получает код из двух цифр типа \(0\!-\!2\), \(3\!-\!7\), \(7\!-\!3\), \(8\!-\!8\) и т. п., позволяющий открывать входную дверь. Хватит ли кодов для всех квартир дома, если в доме \(96\) квартир?
Подсказка
№725 учебника 2023-2026 (стр. 194):
Вспомните:
- Задачи на движение.
- Единицы измерения времени.
- Линейное уравнение с одной переменной.
- Деление и дроби.
- Распределительное свойство умножения.
- Подобные слагаемые.
- Умножение десятичных дробей.
- Сложение десятичных дробей.
- Деление десятичных дробей.
№725 учебника 2014-2022 (стр. 186):
Введите текст
Ответ
№725 учебника 2023-2026 (стр. 194):
\[30\text{ мин}=0{,}5\text{ ч}\]
\(1{,}5+0{,}5=2\text{ (ч)}\) - пешеход был в пути до встречи с велосипедистом.
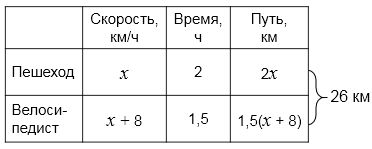
Составим уравнение:
\[2x+1,5(x+8)=26\]
\[2x+1{,}5x+12=26\]
\[3{,}5x+12=26\]
\[3{,}5x=26-12\]
\[3{,}5x=14\]
\(x=\frac{14}{3{,}5}\)
\(x=\frac{140}{35}\)
\(x = 4\)
\(4\) км/ч - скорость пешехода.
\(4+8=12\) (км/ч) - скорость велосипедиста.
Ответ: \(4\) км/ч и \(12\) км/ч.
Пояснения:
Формула пройденного пути:
\[s=vt,\]
где \(t\) — время,
\(s\) — расстояние,
\(v\) — скорость.
\[30\text{ мин}=\frac{30}{60}\text{ ч}=0{,}5\text{ ч}\]
Движение происходит навстречу: пешеход идёт из \(A\) в \(B\), а велосипедист едет из \(B\) в \(A\). До встречи они вместе проходят всё расстояние \(26\) км, поэтому сумма пройденных ими путей равна \(26\).
Пусть скорость пешехода \(x\) км/ч. Тогда по условию скорость велосипедиста \(x+8\) км/ч.
Пешеход вышел раньше на \(30\) минут, то есть на \(0{,}5\) часа. Велосипедист ехал до встречи \(1{,}5\) часа, значит пешеход шёл до встречи:
\[1{,}5+0{,}5=2\text{ ч}.\]
Тогда путь пешехода до встречи равен \(2x,\) а путь велосипедиста до встречи равен \(1,5(x+8).\)
Складываем пути и приравниваем к общему расстоянию:
\[2x+1,5(x+8)=26.\]
Раскрываем скобки, выполняем преобразования и решаем линейное уравнение:
\(3{,}5x=14\), откуда \(x = 4\).
Значит скорость пешехода \(4\) км/ч, а скорость велосипедиста:
\[4+8=12\text{ км/ч}.\]
№725 учебника 2014-2022 (стр. 186):
Первая цифра кода:
\[ 10 \]
Вторая цифра кода:
\[ 10 \]
Количество всех возможных кодов:
\[ 10 \cdot 10 = 100 \]
Сравним с числом квартир:
\[ 100 > 96 \]
Количество лишних кодов:
\[ 100 - 96 = 4 \]
Ответ: кодов хватит.
Пояснения:
В задаче используется правило умножения.
Если первый элемент можно выбрать \(m\) способами, а второй элемент — \(n\) способами, то общее число вариантов равно:
\[ m \cdot n \]
Здесь код состоит из двух цифр.
Для первой цифры можно выбрать любую из цифр:
\[ 0,1,2,3,4,5,6,7,8,9 \]
Это:
\[ 10 \text{ вариантов} \]
Для второй цифры тоже можно выбрать любую из этих десяти цифр.
Это снова:
\[ 10 \text{ вариантов} \]
Поэтому общее число двухзначных кодов равно:
\[ 10 \cdot 10 = 100 \]
Почему здесь именно \(100\), а не меньше?
Потому что по условию:
\[ 7\!-\!3 \text{ и } 3\!-\!7 \]
— это разные коды, значит порядок цифр важен.
Кроме того, допускаются коды с одинаковыми цифрами, например:
\[ 8\!-\!8 \]
Следовательно, все пары цифр от \(00\) до \(99\) подходят, всего их \(100\).
Теперь сравниваем это количество с числом квартир:
\[ 100 \text{ кодов и } 96 \text{ квартир} \]
Так как:
\[ 100 > 96 \]
то кодов достаточно для всех квартир.
Даже останется:
\[ 100 - 96 = 4 \]
свободных кода.
Вернуться к содержанию учебника