Упражнение 199 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник

а) \(y = x|x|\)

Если \(x \ge 0\), то 

\(y = x\cdot x = x^{2}. \)

Если \(x < 0\), то

\(y = x\cdot(-x) = -x^{2}. \)

\( y = \begin{cases} x^{2}, \, если \, x \ge 0,\\[4pt] -x^{2}, \, если \,  x < 0 \end{cases} \)

1) \(y = x^2\), при \( x \ge 0\)

2) \(y = -x^2\), при \( x < 0\)

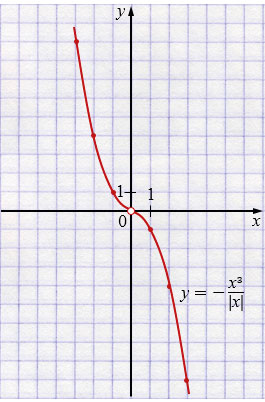
б) \(y = -\dfrac{x^{3}}{|x|}\),     \(x \ne 0\)

Если \(x > 0\), то

\( y = -\dfrac{x^{3}}{x} = -x^{2}. \)

Если \(x < 0\), то

\(y = -\dfrac{x^{3}}{-x} = x^{2}. \)

\( y = \begin{cases} x^{2}, \, если \, x < 0,\\[4pt] -x^{2}, \, если \, x > 0. \end{cases} \)

1) \(y = x^2\), при \( x < 0\)

\((0; 0)\) - выколотая точка.

2) \(y = -x^2\), при \( x > 0\)

Пояснения:

Определение модуля.

Для любого действительного \(x\): \[ |x|= \begin{cases} x, & x\ge 0,\\[4pt] -x, & x<0. \end{cases} \] Это используется, чтобы заменить модуль на обычное выражение и получить формулу без модуля.

Кусочная запись функций.

а) Для \(y = x|x|\) после подстановки модулей получаем две формулы:

\( y=x^{2}\quad (x\ge0),\)

\(y=-x^{2}\quad (x<0). \)

Поэтому график состоит из двух половинок парабол с общей точкой \((0,0)\).

б) Для \(y = -\dfrac{x^{3}}{|x|}\) важно учесть, что при \(x=0\) знаменатель равен нулю, поэтому эта точка исключается. На остальных \(x\) снова получаем две формулы:

\( y=x^{2}\quad (x<0),\)

\(y=-x^{2}\quad (x>0). \)

Здесь график тоже состоит из двух ветвей парабол, но они не соединяются в точке \((0,0)\), так как она не принадлежит графику (выколотая точка).

\( b = \dfrac{4a}{5} \) и \( a > 0 \)

\( \dfrac{(a + b)^{\frac{1}{2}} + (a - b)^{\frac{1}{2}}}{(a + b)^{\frac{1}{2}} - (a - b)^{\frac{1}{2}}} = 2. \)

\( b = \dfrac{4a}{5} \)

\(\dfrac{(a + b)^{\frac{1}{2}} + (a - b)^{\frac{1}{2}}}{(a + b)^{\frac{1}{2}} - (a - b)^{\frac{1}{2}}} = \)

\( =\dfrac{\bigg(a + \dfrac{4a}{5}\bigg)^{\frac{1}{2}} + \bigg(a - \dfrac{4a}{5}\bigg)^{\frac{1}{2}}}{\bigg(a +\dfrac{4a}{5}\bigg)^{\frac{1}{2}} - \bigg(a - \dfrac{4a}{5}\bigg)^{\frac{1}{2}}} = \)

\( =\dfrac{\bigg(\dfrac{9a}{5}\bigg)^{\frac{1}{2}} + \bigg(\dfrac{a}{5}\bigg)^{\frac{1}{2}}}{\bigg(\dfrac{9a}{5}\bigg)^{\frac{1}{2}} - \bigg(\dfrac{a}{5}\bigg)^{\frac{1}{2}}} = \)

\( =\dfrac{\dfrac{(9a)^{\frac{1}{2}}}{5^{\frac{1}{2}}} + \dfrac{a^{\frac{1}{2}}}{5^{\frac{1}{2}}}}{\dfrac{(9a)^{\frac{1}{2}}}{5^{\frac{1}{2}}} - \dfrac{a^{\frac{1}{2}}}{5^{\frac{1}{2}}}} = \)

\(= \dfrac{\frac{3a^{\frac{1}{2}}}{5^{\frac{1}{2}}} + \frac{a^{\frac{1}{2}}}{5^{\frac{1}{2}}}}{\frac{3a^{\frac{1}{2}}}{5^{\frac{1}{2}}} - \frac{a^{\frac{1}{2}}}{5^{\frac{1}{2}}}} = \dfrac{\frac{4a^{\frac{1}{2}}}{5^{\frac{1}{2}}}}{\frac{2a^{\frac{1}{2}}}{5^{\frac{1}{2}}}} = \dfrac{4a^{\frac{1}{2}}}{2a^{\frac{1}{2}}} = 2 \)

\(2=2\) - верно.

Пояснения:

Основные формулы:

Если \(a\) - положительное число, \(\frac{m}{n}\) - дробное число (\(m\) - целое число, \(n\) - натуральное), то  \(a^{\frac{m}{n}}=\sqrt[n]{a^m}.\)

Основные свойства степеней:

Для любого \(a>0\) и  \(b>0\) и любого рационального числа \(p\):

\((ab)^p=a^pb^p,\)

\(\bigg(\frac{a}{b}\bigg)^p=\frac{a^p}{b^p}.\)

Ход решения:

1. Подставляем значение \( b \) в выражения \( a + b \) и \( a - b \).

2. Представляем корни в виде степеней с показателем \( \frac{1}{2} \).

3. Выносим одинаковые множители \( a^{\frac{1}{2}} \) и \( 5^{\frac{1}{2}} \).

4. Сокращаем дробь.

Почему можно сокращать:

Так как \( a > 0 \), то \( a^{\frac{1}{2}} \neq 0 \), значит деление допустимо.

Вывод:

Равенство доказано.