Упражнение 198 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник

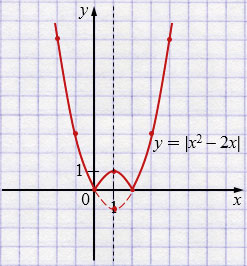
а) \(f(x)=|x^{2}-2x|\)

Нули функции:

\( x^{2}-2x=0\)

\(x(x-2) = 0\)

\(x = 0\)   или   \(x - 2 = 0\)

                       \(x = 2\)

1) Если \(x < 0\), то \(x(x-2)\ge 0\), тогда:

\( f(x)=x^{2}-2x. \)

2) Если  \(0 \le x \le 2\), то \(x(x-2)<0\), тогда:

\( f(x)=-(x^{2}-2x)= -x^{2}+2x. \)

3) Если \(x > 2\), то \(x(x-2)\ge 0\), тогда:

\( f(x)=x^{2}-2x. \)

\(f(x) = \begin{cases} x^{2}-2x, \, если \,  x \le 0,\\[2mm] -x^{2}+2x, \, если \,  0 < x < 2,\\[2mm] x^{2}-2x, \, если \,    x \ge 2 \end{cases}\)

\(y = x^{2}-2x\) - парабола.

1. \(a = 1 > 0\) - ветви параболы направлены вверх.

2. \(x_0 = -\frac{b}{2a} = -\frac{-2}{2} = 1\).

\(y_0 = 1^2 - 2\cdot1 = 1 - 2 = -1\).

\((1; -1)\) - вершина параболы.

\(x = -1\) - ось симметрии параболы.

3. Нули функции: \(x = 0\) и \(x = 2\).

4. Дополнительные точки:

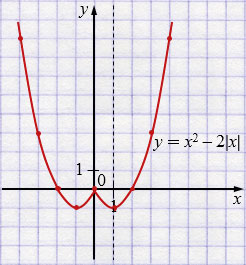
б) \(f(x)=x^{2}-2|x|\)

1) Если \(x\ge 0\), то

\(f(x)=x^{2}-2x. \)

2) Если \(x<0\), то

\( f(x)=x^{2}+2x. \)

\( f(x)= \begin{cases} x^{2}+2x, & x<0,\\[2mm] x^{2}-2x, & x\ge 0. \end{cases} \)

\(y = x^{2}-2x\) - парабола.

1. \(a = 1 > 0\) - ветви параболы направлены вверх.

2. \(x_0 = -\frac{b}{2a} = -\frac{-2}{2} = 1\).

\(y_0 = 1^2 - 2\cdot1 = 1 - 2 = -1\).

\((1; -1)\) - вершина параболы.

\(x = -1\) - ось симметрии параболы.

3. Нули функции: \(x = 0\) и \(x = 2\).

4. Дополнительные точки:

\(y = x^{2}+2x\) - парабола, симметричная параболе \(y = x^{2}-2x\) относительно оси \(y\).

Пояснения:

Если \(y=|f(x)|\), то согласно определению модуля:

\(|f(x)|=\begin{cases} f(x), \, если \,  f(x) \ge 0,\\ -f(x), \, если \,  f(x) < 0. \end{cases} \)

Чтобы построить график функции \(y = |f(x)|\), если известен график функции \(y = f(x)\), нужно оставить на месте ту его часть, где \(f(x) \ge 0\), и симметрично отобразить относительно оси \(x\) другую его часть, где \(f(x) < 0\).

Если \(y=f(|x|)\), то согласно определению модуля:

\(f(|x|)=\begin{cases} f(x), \, если \,  x \ge 0,\\ f(-x), \, если \,  x < 0. \end{cases} \)

Чтобы построить график функции \(y=f(|x|)\), если известен график функции \(y = f(x)\), нужно оставить на месте ту часть графика функции \(y = f(x)\), которая соответствует неотрицательной части области определения функции \(y = f(x)\). Отразив эту часть симметрично относительно оси \(y\) получим другую часть графика, соответствующую отрицательной области определения.

Для пункта а.

Чтобы построить график функции \(f(x)=|x^{2}-2x|\), сначала строим параболу \(y=x^{2}-2x\) (ту часть графика, которая расположена ниже оси \(x\), намечаем пунктиром). Затем строим недостающую часть графика путем симметрии относительно оси \(x\)  - пунктирной части.

Для пункта б.

Чтобы построить график функции \(f(x)=x^{2}-2|x|\), учитывая то, что \(|x|^2 = x^2\), сначала строим параболу \(y=x^{2}-2x\) (ту часть графика, которая расположена левее оси \(y\), не строим). Затем путем симметрии относительно оси \(y\) строим недостающую часть графика.

а) \( u = t^{\frac{2}{3}} + 1, \; v = t^{-\frac{2}{3}} + 1; \)

\( u - 1 = t^{\frac{2}{3}} \)

\( v - 1 = t^{-\frac{2}{3}} = \dfrac{1}{t^{\frac{2}{3}}} \)

\( v - 1 = \dfrac{1}{u - 1} \)

\( v = \dfrac{1}{u - 1} +1 =\dfrac{1}{u - 1}+\dfrac{u - 1}{u - 1}= \)

\(=\frac{1+u-1}{u-1}=\frac{u}{u-1}\)

Ответ: \( v =\frac{u}{u-1}\)

б) \( u = (t + 2)^{\frac{1}{4}}, \; v = (2 - t)^{\frac{1}{4}}. \)

\( u = (t + 2)^{\frac{1}{4}} \)

\( u^4 = t + 2 \)

\( v = (2 - t)^{\frac{1}{4}} \)

\( v^4 = 2 - t \)

\( t = u^4 - 2 \)

\( v^4 = 2 - (u^4 - 2) = 4 - u^4 \)

\( v =\sqrt[4] {4 - u^4} \)

Ответ: \( v =\sqrt[4] {4 - u^4}.\)

Пояснения:

Основная идея:

Нужно избавиться от параметра \( t \), выразив его через одну переменную и подставив в другую.

а) \( u - 1 = t^{\frac{2}{3}}, \quad v - 1 = \frac{1}{t^{\frac{2}{3}}} \)

Следовательно:

\( v - 1 = \frac{1}{u - 1} \)

Откуда:

\( v =\frac{u}{u-1}\)

б) Используем правило:

\( (a^{\frac{1}{4}})^4 = a \)

Получаем:

\( u^4 = t + 2, \quad v^4 = 2 - t \)

Выражаем \( t \):

\[ t = u^4 - 2 \]

Подставляем:

\[ v^4 = 4 - u^4 \]

Откуда:

\( v =\sqrt[4] {4 - u^4}.\)