Упражнение 197 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 69
Вернуться к содержанию учебника
Вопрос
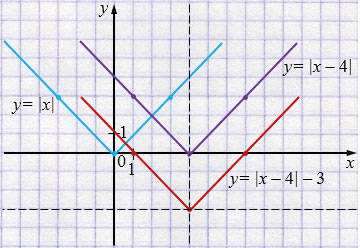
Постройте в одной координатной плоскости графики функций \(y=|x|\), \(y=|x-4|\), \(y=|x-4|-3\).
Подсказка
Вспомните:
- График функции.
- Модуль числа.
- Сдвиги графиков вдоль координатных осей.
- Координаты точки на координатной плоскости.
Ответ
\(y=|x|\)
| \(x\) | \(-3\) | \(0\) | \(3\) |
| \(y\) | \(3\) | \(0\) | \(3\) |
\(y=|x-4|\) - сдвиг графика функции \(y=|x|\) на \(4\) единицы вправо.
\(y=|x-4|-3\) - сдвиг графика функции \(y=|x|\) на \(4\) единицы вправо и на \(3\) единицы вниз.
Пояснения:
Горизонтальные сдвиги (вдоль оси \(x\)):
\( y=f(x-m) \) — сдвиг графика функции \( y=f(x)\) вправо на \(m\) единиц, \(y=f(x+m) \) — сдвиг графика функции \( y=f(x)\) влево на \( m\) единиц.
Вертикальные сдвиги (вдоль оси \(y\)):
\( y=f(x)+n\) — сдвиг графика функции \( y=f(x)\) вверх на \(n\) единиц, \(y=f(x)-k\) — сдвиг графика функции \( y=f(x)\) вниз на \(n\) единиц.
Вершины графиков.
— \(y=|x|\): вершина \((0,0)\);
— \(y=|x-4|\): вершина \((4,0)\);
— \(y=|x-4|-3\): вершина \((4,-3)\).
Все три графика — V-образные ломаные, отличающиеся только сдвигами.
Вернуться к содержанию учебника