Упражнение 1074 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1074 учебника 2023-2025 (стр. 238):
Найдите область определения функции и постройте её график:
а) \(y=\dfrac{x^{2}-9}{6+2x}\);
б) \(y=\dfrac{4-x^{2}}{x^{2}+2x}\).
№1074 учебника 2013-2022 (стр. 248):
Составьте какой-либо ряд, состоящий из пяти чисел. Найдите для него:
а) среднее арифметическое;
б) дисперсию;
в) среднее квадратичное отклонение.
Подсказка
№1074 учебника 2023-2025 (стр. 238):
Вспомните:
- Что такое функция.
- График функции.
- Область определения функции.
- Рациональные дроби.
- Сокращение рациональных дробей.
- Разложение многочлена на множители.
- Разность квадратов двух выражений.
- Линейная функция и ее график.
- Обратная функция и ее график.
- Сложение и вычитание рациональных чисел.
- Деление рациональных чисел.
№1074 учебника 2013-2022 (стр. 248):
Вспомните:
- Что называют средним арифметическим.
- Неправильные дроби.
- Деление и дроби.
- Вычитание рациональных чисел.
- Степень с натуральным показателем.
- Арифметический квадратный корень.
Ответ
№1074 учебника 2023-2025 (стр. 238):
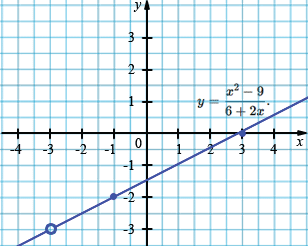
а) \( y=\frac{x^{2}-9}{6+2x}. \)
\(6+2x\neq 0\)
\( x\neq -3. \)
\(D=(- \infty;-3)\cup(-3; +\infty)\)
\( y=\frac{x^{2}-9}{6+2x}=\frac{(x-3)(x+3)}{2(x+3)}\)
\(=\frac{x-3}{2}=0,5x-1,5\)
| \(x\) | -1 | 3 | -3 |
| \(y\) | -2 | 0 | -3 |
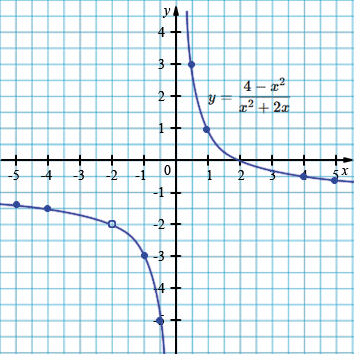
б) \( y=\frac{4-x^{2}}{x^{2}+2x}. \)
\(x^{2}+2x \neq0\)
\(x(x+2)\neq 0\)
\(x\neq 0\) \((x+2)\neq 0\)
\( x\neq 0,\; x\neq -2. \)
\(D=(- \infty;-2)\cup(-2; 0) \cup(0; +\infty)\).
\( y=\frac{4-x^{2}}{x^{2}+2x} = \frac{(2-x)\cancel{(2+x)}}{x\cancel{(x+2)}}= \)
\(= \frac{2-x}{x}= \frac{2}{x}-1\)
| \(x\) | -2 | -5 | -4 | -1 | -0,5 |
| \(y\) | -2 | -1,4 | -1,5 | -3 | -5 |
| \(x\) | 0,5 | 1 | 2 | 4 | 5 |
| \(y\) | 3 | 1 | 0 | -0,5 | -0,6 |
Пояснения:
— Чтобы найти область определения рациональной функции, нужно исключить значения переменной, при которых знаменатель равен нулю.
— В пункте а) исключается только \(x=-3\). Функция сводится к линейной, график — прямая с одной выколотой точкой.
— В пункте б) исключаются \(x=0\) и \(x=-2\). Функция остаётся дробно-рациональной, график является гиперболой с одной выколотой точкой.
№1074 учебника 2013-2022 (стр. 248):
\[ 3,\; 5,\; 7,\; 9,\; 6. \]
а) Среднее арифметическое
\[\frac{3+5+7+9+6}{5} =\frac{30}{5}=6. \]
б) Отклонения от среднего арифметического:
\( 3-6=-3,\)
\(5-6=-1,\)
\(7-6=1,\)
\(9-6=3,\)
\(6-6=0. \)
Сумма квадратов отклонений:
\((-3)^2 + (-1)^2 + 1^2 + 3^2 + 0^2 =\)
\(= 9+1+1+9+0=20. \)
Дисперсия:
\[\frac{20}{5}=4. \]
в) Среднее квадратичное отклонение:
\[ \sigma=\sqrt{4}=2. \]
Пояснения:
Среднее арифметическое — сумма всех элементов ряда, делённая на их количество.
Дисперсия ряда чисел — это среднее арифметическое квадратов отклонений от среднего арифметического этого ряда.
Среднее квадратичное отклонение — квадратный корень из дисперсии.
Вернуться к содержанию учебника