Упражнение 995 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

\(x^2+2ax+a^2-4=0\)

 \(A=1,\; B=2a,\; C=a^2-4.\)

\(D=B^2-4AC=\)

\(=(2a)^2-4\cdot 1\cdot(a^2-4)=\)

\(=4a^2-4a^2+16=16 > 0\) - уравнение имеет 2 корня.

\(\sqrt D = 4\)

\( x_{1}= \frac{-2a + 4}{2} =\frac{\cancel2(-a + 2)}{\cancel2} =\)

\(=-a + 2. \)

\( x_{2}= \frac{-2a - 4}{2} =\frac{\cancel2(-a - 2)}{\cancel2} =\)

\(=-a - 2. \)

1) \(x_1 \in (-6;6)\)

\(-6 < -a + 2 < 6\)

\(\begin{cases} -a + 2 > -6,\\ -a + 2 < 6 \end{cases}\)

\(\begin{cases} -a > -6 - 2,\\ -a < 6 - 2 \end{cases}\)

\(\begin{cases} -a > -8, /\times(-1) \\ -a < 4 /\times(-1) \end{cases}\)

\(\begin{cases} a < 8, \\ a > -4 \end{cases}\)

\(a \in (-4; 8)\)

2) \(x_2 \in (-6;6)\)

\(-6 < -a - 2 < 6\)

\(\begin{cases} -a - 2 > -6,\\ -a - 2 < 6 \end{cases}\)

\(\begin{cases} -a > -6 + 2,\\ -a < 6 + 2 \end{cases}\)

\(\begin{cases} -a > --4, /\times(-1) \\ -a < 8 /\times(-1) \end{cases}\)

\(\begin{cases} a < 4, \\ a > -8 \end{cases}\)

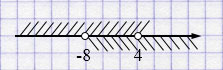
\(a \in (-8; 4)\)

3)

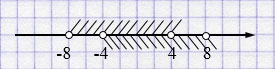
\((-4; 8) \cap (-8; 4) = (-4; 4)\)

Ответ: \(a \in (-4; 4\).

Пояснения:

При решении учитываем то, что квадратное уравнение

\(Ax^2 + Bx + C=0\) имеет два корня в том случае, когда дискриминант

\(D = B^2-4AC > 0\), и тогда корни уравнения:

\(x_{1,2} =\frac{-B \pm \sqrt D}{2A}\).

По условию корни уравнения должны принадлежать промежутку \((-6; 6)\). Поэтому, найдя корни уравнения \(x_1\) и \(x_2\), мы рассматриваем два двойных неравенства относительно \(a\) и находим пересечение решений этих неравенств.

Двойное неравенство удобно раскладывать на систему из двух простых неравенств:

1) средняя часть больше левой части;

2) средняя часть меньше правой.

Чтобы решить систему неравенств, нужно найти пересечение решений неравенств системы, то есть найти множество чисел, которое является одновременно решением и одного неравенства и решением другого неравенства. Если решения неравенств не пересекаются, то система решений не имеет.

При решении неравенств системы используем то, что:

- если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство;

- если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное ему неравенство.

- если обе части неравенства разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное ему неравенство.

Если знак неравенства строгий (\(>\)  или \(<\)), то точку на координатной прямой делаем "выколотой" (незакрашенной), при записи промежутка используем круглую скобку.

Если знак неравенства нестрогий (\(\geq\)  или \(\leq\)), то точку на координатной прямой делаем закрашенной, а при записи промежутка используем квадратную скобку.

а) \(\dfrac{25^{m}}{5^{2m-1}}=\dfrac{(5^2)^{m}}{5^{2m-1}}=\dfrac{5^{2m}}{5^{2m-1}}=\)

\(=5^{2m -(2m-1)} = 5^{\cancel{2m}-\cancel{2m}+1} =5^1 = 5\)

б) \(\dfrac{6^{m}}{2^{\,m-1}\cdot 3^{\,m+1}}=\dfrac{(2\cdot3)^{m}}{2^{\,m-1}\cdot 3^{\,m+1}}=\)

\(=\dfrac{2^{m}3^{m}}{2^{m-1}3^{m+1}}=\)

\(=2^{\,m-(m-1)}\cdot3^{\,m-(m+1)}=\)

\(=2^{\,m-m+1}\cdot3^{\,m-m-1}=\)

\(=2^1\cdot3^{-1} = 2\cdot\frac13=\dfrac{2}{3}\).

Пояснения:

Используемые свойства степеней:

\(a^{m}\cdot a^{n}=a^{m+n},\)

\(\frac{a^{m}}{a^{n}}=a^{m-n},\)

\((a^{m})^{n}=a^{mn},\)

\((ab)^m = a^mb^m.\)