Упражнение 827 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

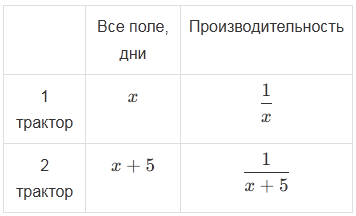
Составим уравнение:

\(\frac{1}{x} + \frac{1}{x+5}= \frac{2}{3} : 4\)

\(\frac{1}{x} + \frac{1}{x+5} = \frac{\cancel2}{3} \cdot \frac{1}{\cancel4_2}\)

\(\frac{1}{x} + \frac{1}{x+5} = \frac{1}{6}\)  \(/\times 6x(x+5)\)

ОДЗ: \(x\neq0\)   и   \(x + 5\neq 0\)

                            \(x\neq-5\)

\(6(x + 5) + 6x = x(x+5)\)

\(6x + 30 + 6x = x^2 +5x\)

\(12x + 30 = x^2 +5x\)

\(x^2 + 5x-12x - 30 = 0\)

\(x^2-7x -30 = 0\)

\(a = 1\),  \(b = -7\),  \(c = -30\)

\(D = b^2 - 4ac = \)

\(=(-7)^2 - 4\cdot1\cdot(-30)=\)

\(=49 + 120 = 169\),    \(\sqrt D 13\).

\(x_1 = \frac{-(-7) + 13}{2\cdot1}=\frac{20}{2} = 10\).

\(x_2 = \frac{-(-7) - 13}{2\cdot1}=\frac{-6}{2} = -3\) - не удовлетворяет условию.

1) За \(10\) дней вспашет все поле первый трактор.

2)  \(10+5=15\) (дней) - вспашет все поле второй трактор.

Ответ: первый трактор — 10 дней, второй трактор — 15 дней.

Пояснения:

1. В задаче используется понятие производительности:

\(\text{Работа} = \text{Производительность} \times \text{Время}\).

Если первый трактор пашет за \(x\) дней, то его производительность \(\frac{1}{x}\), второй пашет за \(x+5\), производительность \(\frac{1}{x+5}\).

Совместная работа за 4 дня равна \(\frac{2}{3}\). Следовательно, можем составить дробное рациональное уравнение:

\(\frac{1}{x} + \frac{1}{x+5}= \frac{2}{3} : 4\)

Алгоритм решения дробного рационального уравнений:

1) найти ОДЗ (область допустимых значений), то есть те значения переменной, при которых знаменатель обращается в нуль;

2) найти общий знаменатель дробей, входящих в уравнение;

3) умножить обе части уравнения на общий знаменатель;

4) решить получившееся целое уравнение;

5) исключить из его корней те, которые совпадают с ОДЗ.

После того как обе части уравнения домножили на общий знаменатель и выполнили преобразования, получили квадратное уравнение, у которого дискриминант \(D = b^2 - 4ac>0\), поэтому уравнение имеет два корня: \(10\) и \(-3\). Но отрицательный корень не подходит, так как время не может быть отрицательным числом.

Значит, первый трактор пашет поле за 10 дней, а второй — за 15 дней, так как первым можно вспахать поле на 5 дней быстрее, чем вторым.

а) \([-7; 0]\) и \([-3; 5]\)

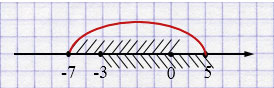
\([-7; 0] \cup [-3; 5] = [-7; 5]\)

Ответ: \( [-7; 5]\).

б) \((-4; 1)\) и \((10; 12)\)

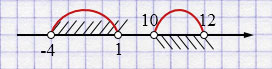
\((-4; 1) \cup (10; 12)\)

Ответ: \((-4; 1) \cup (10; 12)\).

в) \((-\infty; 4)\) и \((10; +\infty)\)

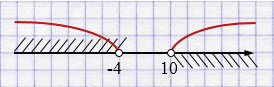
\((-\infty; 4) \cup (10; +\infty)\)

Ответ: \((-\infty; 4) \cup (10; +\infty)\).

г) \([3; +\infty)\) и \((8; +\infty)\)

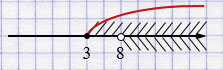
\([3; +\infty) \cup (8; +\infty) = [3; +\infty)\).

Ответ: \([3; +\infty)\).

Пояснения:

Объединение двух промежутков — это множество чисел, которые принадлежат хотя бы одному из них.