Упражнение 864 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник. Страница 193
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№864 учебника 2023-2025 (стр. 193):
Используя свойства неравенств, запишите верное неравенство, которое получится, если:
а) к обеим частям неравенства \(18 > -7\) прибавить число \(-5\); число \(2{,}7\); число \(7\);
б) из обеих частей неравенства \(5 > -3\) вычесть число \(2\); число \(12\); число \(-5\);
в) обе части неравенства \(-9 < 21\) умножить на \(2\); на \(-1\); на \(-\frac{1}{3}\);
г) обе части неравенства \(15 > -6\) разделить на \(3\); на \(-3\); на \(-1\).
№864 учебника 2013-2022 (стр. 193):
Найдите множество значений \(k\), при которых уравнение
\[(k - 4)x^2 + 16x - 24 = 0\]
имеет два корня.
Подсказка
№864 учебника 2023-2025 (стр. 193):
Вспомните:
- Свойства числовых неравенств.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Умножение рациональных чисел.
- Деление рациональных чисел.
- Сложение и вычитание десятичных дробей.
- Умножение обыкновенных дробей.
№864 учебника 2013-2022 (стр. 193):
Вспомните:
- Решение полных квадратных уравнений.
- Решение неравенств с одной переменной.
- Числовые промежутки.
- Деление и дроби.
- Сокращение дробей.
- Степень с натуральным показателем.
- Распределительное свойство умножения.
- Неправильные дроби.
- Смешанные числа.
Ответ
№864 учебника 2023-2025 (стр. 193):
а) \( 18 > -7\)
1) \(18+(-5) > -7+(-5)\)
\(13 > -12\)
2) \( 18 + 2,7 > -7 + 2,7\)
\(20{,}7 > -4{,}3\)
3) \( 18 + 7 > -7 + 7\)
\(25 > 0\).
б) \( 5 > -3\)
1) \( 5 - 2 > -3 - 2\)
\(3 > -5\).
2) \( 5 - 12 > -3 - 12\)
\(-7 > -15\).
3) \( 5 - (-5) > -3 - (-5)\)
\(10 > 2\).
в) \( -9 < 21\)
1) \( -9\cdot2 < 21 \cdot 2\)
\(-18 < 42\).
2) \( -9\cdot (-1) < 21 \cdot (-1)\)
\(9 > -21\)
3) \( -9\cdot (-\frac13) < 21 \cdot (-\frac13)\)
\(3 > -7\)
г) \( 15 > -6\)
1) \( 15 : 3 > -6 : 3\)
\(5 > -2\).
2) \( 15 : (-3) > -6 : (-3)\)
\(-5 < 2\)
3) \( 15 : (-1) > -6 : (-1)\)
\(-15 < 6\)
Пояснения:
1. Если к обеим частям неравенства прибавить или вычесть одно и то же число, знак неравенства сохраняется.
2. Если обе части неравенства умножить или разделить на одно и то же положительное число, знак неравенства сохраняется.
3. Если обе части неравенства умножить или разделить на одно и то же отрицательное число, знак неравенства меняется на противоположный.
№864 учебника 2013-2022 (стр. 193):
\((k-4)x^2 + 16x - 24 = 0\).
\(A = k-4,\; B = 16,\; C = -24\).
\(k-4 \neq 0 \)
\(k \neq 4\).
\(D = B^2 - 4AC =\)
\(=16^2 - 4(k-4)(-24)=\)
\( = 256 - 4(k-4)(-24)=\)
\( = 256 + 96(k-4)=\)
\( = 256 + 96k - 384=\)
\( = 96k - 128\).
Уравнение имеет два корня при \(D > 0\).
\(96k - 128 > 0\)
\(96k > 128\) \(/ : 96\)
\(k > \frac{128}{96}\)
\(k > \frac{4}{3}\)
\(k > 1\frac{1}{3}\).
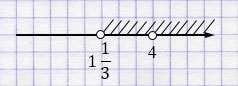
Ответ: \( (1\frac{1}{3}; 4) \cup (4; +\infty)\).
Пояснения:
Для квадратного уравнения \(Ax^2 + Bx + C = 0\) количество корней определяется дискриминантом:
\[D = B^2 - 4AC\]
- \(D > 0\) — два различных корня;
- \(D = 0\) — один корень;
- \(D < 0\) — нет корней.
Кроме того, уравнение должно оставаться квадратным, поэтому
\(A \neq 0\), что выполняется при \(k \neq 4\).
В задаче получили дискриминант
\(D = 96k - 128\). Для двух корней необходимо \(D > 0\), то есть
\(96k - 128 > 0\).
При решении неравенства использовали то, что:
- если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство;
- если обе части неравенства разделить на одно и то же положительное число, то получится равносильное ему неравенство.
Решив неравенство, получили \(k > 1\frac{1}{3}\). Значит, множество значений параметра \(k\), при которых уравнение имеет два корня определяется объединением промежутков \( (1\frac{1}{3}; 4) \cup (4; +\infty)\).
Вернуться к содержанию учебника