Упражнение 863 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник. Страница 193

а) \(a - 3 > b - 3\) и \(b > 4\)

\( a > b\)

\(b>0\),   \(a > 0\)

Ответ: \(a\) и \(b\) - положительные числа.

б) \(a - 8 > b - 8\) и \(a < -12\)

\( a > b\)

\(a<0\),   \(b < 0\).

Ответ: \(a\) и \(b\) - отрицательные числа.

в) \(7a > 7b\) и \(b > \frac{1}{2}\)

\( a > b\)

\(b>0\),   \(a > 0\)

Ответ: \(a\) и \(b\) - положительные числа.

г) \(-2a > -2b\) и \(b < -\frac{1}{3}\)

\(a < b\)

\(b < 0\),   \(a<0\).

Ответ: \(a\) и \(b\) - отрицательные числа.

Пояснения:

Использованные свойства:

1) если к обеим частям верного неравенства прибавить (вычесть) одно и то же число, то получится верное неравенство.

2) если обе части верного неравенства умножить или разделить на одно и то же положительное число, то получится верное неравенство;

3) если обе части верного неравенства умножить или разделить на одно и то же отрицательное число и изменить знак неравенства на противоположный, то получится верное неравенство.

\((a+5)x^2 + 4x - 20 = 0\)

\(A = a+5,\; B = 4,\; C = -20\).

\(D = B^2 - 4AC =\)

\(=4^2 - 4(a+5)(-20)=\)

\( = 16 - 4(a+5)(-20)=\)

\( = 16 + 80(a+5)=\)

\( = 16 + 80a + 400=\)

\( = 80a + 416\).

Уравнение не имеет корней при

\(D < 0.\)

\( 80a + 416 < 0\)

\(80a < -416\)   \(/ : 80\)

\(a < -\frac{416}{80}\).

\(a < -\frac{26}{5}\).

\(a < 5,2\)

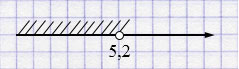
Ответ: \((-\infty; 5,2)\).

Пояснения:

Для квадратного уравнения

\(Ax^2 + Bx + C = 0\) наличие решений зависит от дискриминанта:

\[D = B^2 - 4AC\]

- Если \(D > 0\), уравнение имеет два различных корня.

- Если \(D = 0\), уравнение имеет один корень.

- Если \(D < 0\), то корней нет.

В данной задаче коэффициенты зависят от переменной \(a\). Поэтому условие отсутствия корней сводится к неравенству \(D < 0\).

Мы нашли, что дискриминант равен \(D = 80a + 416\).

При решении неравенства использовали то, что:

- если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство;

- если обе части неравенства разделить на одно и то же положительное число, то получится равносильное ему неравенство.

Решив неравенство \(80a + 416 < 0\), получили \(a < 5,2\). Значит, множество значений параметра \(a\), при которых уравнение не имеет корней определяется промежутком \((-\infty; 5,2)\).