Упражнение 861 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№861 учебника 2023-2025 (стр. 192):
Пусть \(m, n, p\) и \( q\) — некоторые числа, причём \(m > p\), \(n > m\), \(n < q\). Сравните, если это возможно, числа \(p\) и \(n\), \(p\) и \(q\), \(q\) и \(m\). При сравнении чисел воспользуйтесь координатной прямой.
№861 учебника 2013-2022 (стр. 193):
Найдите:
а) наибольшее целое число, удовлетворяющее неравенству \(1{,}6 - (3 - 2y) < 5\);
б) наименьшее целое число, удовлетворяющее неравенству \(8(6 - y) < 24{,}2 - 7y\).
Подсказка
№861 учебника 2023-2025 (стр. 192):
Вспомните положение чисел на координатной прямой.
№861 учебника 2013-2022 (стр. 193):
Вспомните:
- Целые числа.
- Решение неравенств с одной переменной.
- Числовые промежутки.
- Деление и дроби.
- Деление десятичных дробей.
- Сложение и вычитание десятичных дробей.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Деление рациональных чисел.
- Раскрытие скобок, подобные слагаемые.
- Распределительное свойство умножения.
Ответ
№861 учебника 2023-2025 (стр. 192):
\(m > p\), \(n > m\), \(n < q\)
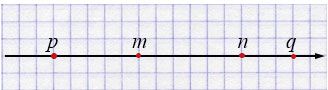
\(p < n\), \(p < q\), \(q > m.\)
Пояснения:
Даны условия:
1) \(m > p\) — значит, \(p\) левее \(m\);
2) \(n > m\) — значит, \(n\) правее \(m\);
3) \(n < q\) — значит, \(q\) находится правее \(n\).
Тогда расположение на прямой:
\[ p < m < n
Сравнения:
- \(p\) левее \(n\), значит, \(p < n\);
- \(p\) левее \(q\), значит, \(p < q\);
- \(q\) правее \(m\), значит, \(q > m.\)
№861 учебника 2013-2022 (стр. 193):
а) \(1,6 - (3 - 2y) < 5\)
\(1,6 - 3 + 2y < 5\)
\(2y - 1,4 < 5\)
\(2y < 5+1,4\)
\(2y < 6,4\) \(/ : 2\)
\(y < 3,2\)
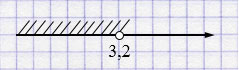
\(y \in (-\infty; 3,2)\).
Ответ: наибольшее целое \(y = 3\).
б) \(8(6 - y) < 24,2 - 7y\)
\(48 - 8y < 24,2 - 7y\)
\(- 8y + 7y < 24,2 - 48\)
\(- y < -23,8\) \(/ : (-1)\)
\(y > 23,8\)
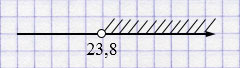
\(y \in (23,8; +\infty)\).
Ответ: наименьшее целое \(y = 24\).
Пояснения:
Чтобы определить наибольшее или наименьшее значение переменной, удовлетворяющей неравенству, нужно решить неравенство и из промежутка, который является решением этого неравенства выбрать наибольшее или наименьшее значение.
При решении неравенств сначала раскрываем скобки и приводим подобные слагаемые. В пункте а) учитываем то, что знак минус перед скобками при их раскрытии меняет все знаки в скобках на противоположные. В пункте б) используем распределительное свойство умножения.
Затем при решении неравенств используем то, что:
- если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство;
- если обе части неравенства разделить на одно и то же положительное число, то получится равносильное ему неравенство;
- если обе части неравенства разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное ему неравенство.
Если знак неравенства нестрогий (\(\geq\) или \(\leq\)), то точку на координатной прямой делаем закрашенной, а при записи промежутка используем квадратную скобку.
У \(-\infty\) и \(+\infty\) при записи промежутка скобка всегда круглая.
Вернуться к содержанию учебника