Упражнение 869 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник. Страница 194
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№869 учебника 2023-2025 (стр. 194):
Известно, что \(a, b, c\) и \( d\) — положительные числа, причём \(a > b\), \(d < b\), \(c > a\). Расположите в порядке возрастания числа:
\(\dfrac{1}{a}, \dfrac{1}{b}, \dfrac{1}{c}, \dfrac{1}{d}\).
№869 учебника 2013-2022 (стр. 194):
Туристы отправились на моторной лодке по течению реки и должны вернуться обратно к стоянке не позднее чем через 3 ч. На какое расстояние могут отъехать туристы, если скорость течения реки 2 км/ч, а скорость лодки в стоячей воде 18 км/ч?
Подсказка
№869 учебника 2023-2025 (стр. 194):
Вспомните:
№869 учебника 2013-2022 (стр. 194):
Вспомните:
Ответ
№869 учебника 2023-2025 (стр. 194):
\(a > b \), тогда \( \dfrac{1}{a} < \dfrac{1}{b}\).
\(d < b\), тогда \( \dfrac{1}{d} > \dfrac{1}{b}\).
\(c > a \), тогда \( \dfrac{1}{c} < \dfrac{1}{a}\).
\(\dfrac{1}{c} < \dfrac{1}{a} < \dfrac{1}{b} < \dfrac{1}{d}\).
Пояснения:
Используем свойство обратных величин: если \(x\) и \(y\) - положительные числа и \(x < y\), то \(\dfrac{1}{x} > \dfrac{1}{y}\).
\(a > b\), \(d < b\), \(c > a\)
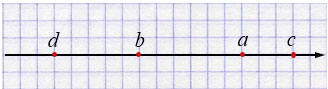
\(d < b < a < c\)
\(\dfrac{1}{c} < \dfrac{1}{a} < \dfrac{1}{b} < \dfrac{1}{d}\).
№869 учебника 2013-2022 (стр. 194):
Пусть расстояние, на которое могут отъехать туристы \(x\) км.
Скорость лодки по течению:
\(18 + 2 = 20\) (км/ч).
Скорость лодки против течения:
\(18 - 2 = 16\) (км/ч).
Время на путь по течению: \(\frac{x}{20}\) ч.
Время в путь против течения: \(\frac{x}{16}\) ч.
Известно, что общее время в пути должно быть не более 3 ч.
Составим неравенство:
\(\frac{x}{20} + \frac{x}{16} \leq 3\) \(/\times 80\)
\(4x + 5x \leq 240\)
\(9x \leq 240\) \(/ : 9\)
\(x \leq \frac{240}{9}\)
\(x \leq \frac{80}{3}\)
\(x \leq 26\frac{2}{3}\)
Ответ: туристы могут отъехать на расстояние не более \( 26\frac{2}{3}\) км.
Пояснения:
При решении задачи учитывается, что скорость лодки относительно берега изменяется из-за течения реки:
- по течению: \(v_{лодки} + v_{течения}\);
- против течения: \(v_{лодки} - v_{течения}\).
Время движения рассчитывается по формуле:
\[t = \frac{s}{v},\]
где \(s\) — путь, \(v\) — скорость.
Так как общее время движения ограничено 3 часами, составили неравенство:
\[\frac{x}{20} + \frac{x}{16} \leq 3.\]
Если обе части неравенства разделить на одно и то же положительное число, то получится равносильное ему неравенство. Поэтому, домножив обе части неравенства на общий знаменатель дробей 80, избавились от знаменателей:
\(4x + 5x \leq 240\),
\(9x \leq 240\).
Если обе части неравенства разделить на одно и то же положительное число, то получится равносильное ему неравенство. Разделив обе части неравенства на 9, получили \(x \leq 26\frac{2}{3}\).
Следовательно, туристы могут отъехать на расстояние не более \( 26\frac{2}{3}\) км.
Вернуться к содержанию учебника