Упражнение 652 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник. Страница 140
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№652 учебника 2023-2025 (стр. 140):
Решите уравнение:
а) \(\displaystyle \frac{3x+5}{5} \;-\;\frac{x+1}{3} = 1;\)
б) \(\displaystyle \frac{2p-1}{6} \;-\;\frac{p+1}{3} = p;\)
в) \(\displaystyle \frac{6y-1}{15} \;-\;\frac{y}{5} = \frac{2y}{3};\)
г) \(\displaystyle \frac{12 - x}{4} \;-\;\frac{2 - x}{3} = \frac{x}{6}.\)
№652 учебника 2013-2022 (стр. 140):
Решите графически уравнение
\[x^2 = 6 - x.\]
Подсказка
№652 учебника 2023-2025 (стр. 140):
Вспомните:
- Что значит решить уравнение.
- Линейные уравнения.
- Свойства уравнений.
- Раскрытие скобок, подобные слагаемые.
- Деление и дроби.
- Умножение рациональных чисел.
- Деление рациональных чисел.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Противоположные числа.
- Десятичная запись дробных чисел.
- Деление десятичных дробей.
- Наименьшее общее кратное.
- Сокращение обыкновенных дробей.
№652 учебника 2013-2022 (стр. 140):
Вспомните:
Ответ
№652 учебника 2023-2025 (стр. 140):
а) \( \frac{3x+5}{5} - \frac{x+1}{3} = 1;\) \(|\times15\)
\( 3(3x+5) - 5(x+1) = 15;\)
\(9x + 15 - 5x - 5 = 15;\)
\(4x + 10 = 15;\)
\(4x= 15 -10;\)
\(4x = 5;\)
\(x = \frac{5}{4};\)
| - | 5 | 4 | ||||||||||||
| 4 | 1 | , | 2 | 5 | ||||||||||
| - | 1 | 0 | ||||||||||||
| 8 | ||||||||||||||
| - | 2 | 0 | ||||||||||||
| 2 | 0 | |||||||||||||
| 0 |
\(x=1,25.\)
Ответ: \(x=1,25.\)
б) \(\frac{2p-1}{6} - \frac{p+1}{3} = p;\) \(|\times6\)
\((2p-1) - 2(p+1) = 6p;\)
\(2p - 1 - 2p - 2 = 6p;\)
\(-3 = 6p;\)
\(p = -\frac{3}{6};\)
\(p = -0,5.\)
Ответ: \(p = -0,5.\)
в) \( \frac{6y-1}{15} - \frac{y}{5} = \frac{2y}{3};\) \(|\times15\)
\(6y-1 - 3y = 10y;\)
\(6y - 3y - 10y = 1;\)
\(-7y = 1;\)
\(y = -\frac{1}{7}. \)
Ответ: \(y = -\frac{1}{7}. \)
г) \( \frac{12 - x}{4} - \frac{2 - x}{3} = \frac{x}{6};\) \(|\times12\)
\(3(12 - x) - 4(2 - x) = 2x;\)
\(36 - 3x - 8 + 4x = 2x;\)
\(28 + x = 2x;\)
\(x = 28. \)
Ответ: \(x = 28. \)
Пояснения:
Во всех пунктах первым шагом умножаем обе части уравнения на наименьшее общее кратное знаменателей, чтобы «сократить» дроби и перейти к линейному уравнению без дробей.
Далее раскрываем скобки (если есть), приводим подобные слагаемые. Слагаемые, содержащие переменную, переносим влево, остальные - вправо, если есть подобные - приводим. Данные шаги позволяют получить линейное уравнение вида \(a\,x = b\), корень которого: \(x = \frac{b}{a}\).
№652 учебника 2013-2022 (стр. 140):
\(y = x^2\)
| 0 | 1 | -1 | 2 | -2 | 3 | -3 | 4 | -4 | |
| 0 | 1 | 1 | 4 | 4 | 9 | 9 | 16 | 16 |
\(y = 6 - x\)
| 0 | 2 | |
| 6 | 4 |
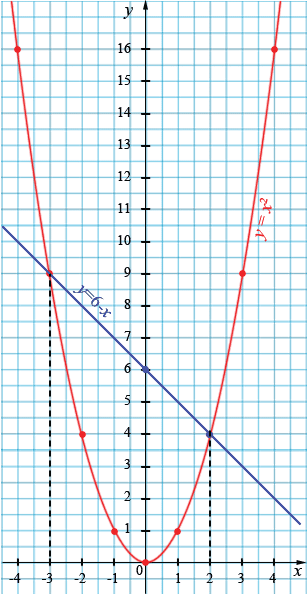
\( x = 2 \) и \(x = -3\).
Ответ: \(x = 2\) и \(x = -3\).
Пояснения:
1) Графический метод состоит в нахождении точек пересечения графиков функций \(y = f(x)\) и \(y = g(x)\), где уравнение \(f(x) = g(x)\).
2) В нашем случае \(f(x) = x^2\) (ветви параболы вверх, вершина в начале координат) и \(g(x) = 6 - x\).
3. Эти графики пересекаются в двух точках. Абсциссы точек пересечения графиков являются теми значениями переменной \(x\), при которых выражения \(x^2\) и \(6-x\) принимают равные значения. Значит, абсциссы точек пересечения являются корнями уравнения \(x^2=6-x.\)
4) Из рисунка видно, что это уравнение имеет корни: \(\;2\) и \(-3\).
Вернуться к содержанию учебника