Рациональные числа
Вместе целые и дробные числа образуют рациональные числа.
Число, которое можно записать в виде отношения 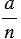 , где , где 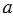 - целое число, а - целое число, а 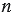 - натуральное число, называют рациональным числом. - натуральное число, называют рациональным числом. |
Нам известно, что любое целое число 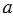 можно записать в виде
можно записать в виде 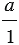 ,
, 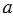 - целое число, 1 - это натуральное число, значит, любое целое число является рациональным числом.
- целое число, 1 - это натуральное число, значит, любое целое число является рациональным числом.
Примеры:
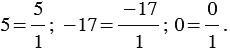
Рассмотрим дробь: 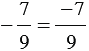 ,
, 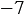 - целое число,
- целое число, 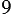 - натуральное число.
- натуральное число.
То есть любая отрицательная дробь является рациональным числом.
Любое смешанное число и любая десятичная дробь также являются рациональными числами.
Примеры:
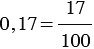 , 17 - целое число, 100 - натуральное число.
, 17 - целое число, 100 - натуральное число.
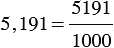 , 5191 - целое число, 1000 - натуральное число.
, 5191 - целое число, 1000 - натуральное число.
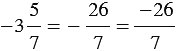 ,
,  26 - целое число, 7 - натуральное число.
26 - целое число, 7 - натуральное число.
Рассмотрим разность, сумму и произведение двух рациональных чисел:
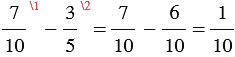 , 1 - целое число, 10 - натуральное число.
, 1 - целое число, 10 - натуральное число.
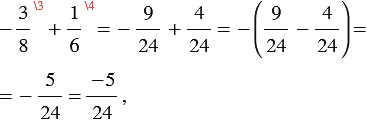
 5 - целое число, 24 - натуральное число.
5 - целое число, 24 - натуральное число.
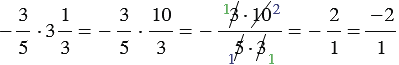 ,
,
 2 - целое число, 1 - натуральное число.
2 - целое число, 1 - натуральное число.
То есть сумма, разность и произведение рациональных чисел являются рациональными числами.
Если делитель отличен от нуля, то частное двух рациональных чисел тоже рациональное число.
Пример:
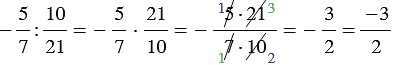 ,
,
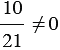 ,
,  3 - целое число, 2 - натуральное число.
3 - целое число, 2 - натуральное число.
Нам известно, что обыкновенную дробь можно представить в виде десятичной дроби, разделив ее числитель на знаменатель, например:
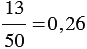 , так как 13 : 50 = 0,26.
, так как 13 : 50 = 0,26.
| - | 1 | 3 | 0 | 0 | 5 | 0 | |||
| 1 | 0 | 0 | 0 | 2 | 6 | ||||
| - | 3 | 0 | 0 | ||||||
| 3 | 0 | 0 | |||||||
| 0 |
Нам также известно, что не любую обыкновенную дробь можно представить в виде десятичной дроби, например, если нам дана дробь 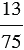 , то при делении числителя на знаменатель мы получим сначала нуль целых, потом одну десятую, семь сотых , три тысячных и дальше при делении все время будут повторятся остаток 25 и в частном цифра 3.
, то при делении числителя на знаменатель мы получим сначала нуль целых, потом одну десятую, семь сотых , три тысячных и дальше при делении все время будут повторятся остаток 25 и в частном цифра 3.
| - | 1 | 3 | 7 | 5 | |||||||||
| 7 | 5 | 0 | , | 1 | 7 | 3 | 3 | . | . | ||||
| - | 5 | 5 | 0 | ||||||||||
| 5 | 2 | 5 | |||||||||||
| - | 2 | 5 | 0 | ||||||||||
| 2 | 2 | 5 | |||||||||||
| - | 2 | 5 | 0 | ||||||||||
| 2 | 2 | 5 | |||||||||||
| 2 | 5 |
Данное деление никогда не кончится, то есть дробь 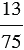 нельзя представить в виде десятичной дроби. При этом если разрешить писать бесконечные дроби, то
нельзя представить в виде десятичной дроби. При этом если разрешить писать бесконечные дроби, то 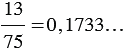 .
.
Рассмотрим дроби 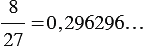 ,
, 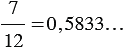 ,
, 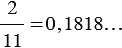 , в записях данных дробей одна или несколько цифр начинают повторяться бесконечно много раз. Такого вида записи называют периодическими дробями, при этом вместо 0,296296... пишут 0,(296), вместо 0,5833... пишут 0,58(3), вместо 0,1818... пишут 0,(18).
, в записях данных дробей одна или несколько цифр начинают повторяться бесконечно много раз. Такого вида записи называют периодическими дробями, при этом вместо 0,296296... пишут 0,(296), вместо 0,5833... пишут 0,58(3), вместо 0,1818... пишут 0,(18).
| Любое рациональное число можно записать в виде десятичной дроби (в частности целого числа), либо в виде периодической дроби. |
Для дроби 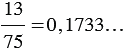 число 0,173 является приближённым значением до тысячных с недостатком: 0,173 <
число 0,173 является приближённым значением до тысячных с недостатком: 0,173 < 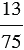 . Число 0,174 является приближённым значением этой дроби до тысячных с избытком:
. Число 0,174 является приближённым значением этой дроби до тысячных с избытком: 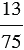 < 0,174. То есть получаем, что 0,173 <
< 0,174. То есть получаем, что 0,173 < 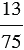 < 0,174.
< 0,174.
Советуем посмотреть:
Положительные и отрицательные числа. Координаты на прямой
Свойства действий с рациональными числами
Правило встречается в следующих упражнениях:
5 класс
Задание 4, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
6 класс
Номер 1125, Мерзляк, Полонский, Якир, Учебник
Номер 1177, Мерзляк, Полонский, Якир, Учебник
Номер 1193, Мерзляк, Полонский, Якир, Учебник
Номер 4, Мерзляк, Полонский, Якир, Учебник
Задание 1182, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1241, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1243, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1257, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание стр. 72, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 4.350, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
7 класс
Номер 3, Мерзляк, Полонский, Якир, Учебник
Номер 6, Мерзляк, Полонский, Якир, Учебник
Номер 21, Мерзляк, Полонский, Якир, Учебник
Номер 25, Мерзляк, Полонский, Якир, Учебник
Номер 117, Мерзляк, Полонский, Якир, Учебник
Номер 118, Мерзляк, Полонский, Якир, Учебник
Номер 127, Мерзляк, Полонский, Якир, Учебник
Упражнение 1, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 5, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 254, Макарычев, Миндюк, Нешков, Суворова, Учебник
8 класс
Номер 3, Мерзляк, Полонский, Якир, Учебник
Номер 5, Мерзляк, Полонский, Якир, Учебник
Номер 6, Мерзляк, Полонский, Якир, Учебник
Упражнение 276, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 467, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 478, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 492, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1287, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение стр. 85, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 267, Макарычев, Миндюк, Учебник
9 класс