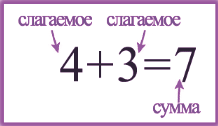Сложение натуральных чисел
К нескольким натуральным числам прибавим 1:
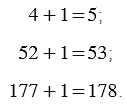
Мы видим, что когда мы прибавляем к натуральному числу 1, получаем следующее за ним натуральное число, т.е. следующее число больше предыдущего на единицу. Теперь к 4 прибавим 3: 4+3: для этого к 4 прибавим 3 раза единицу. Учитывая, что при прибавлении к числу единицы получаем следующее число, получим:
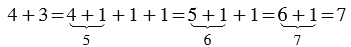
Но мы записываем коротко: 4+3=7.
|
Запомните: Числа, которые складываются, называются слагаемыми, число, которое получается в результате сложения, называется суммой.
|
Сложение чисел на координатном луче
Изобразим координатный луч. Отметим на нем начало координат, единичный отрезок и несколько чисел, следующих друг за другом:
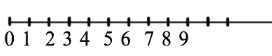
Рассмотрим наш пример: 4+3. Для того чтобы к 4 прибавить 3 на координатном луче, необходимо от точки 4 вправо отложить 3 единичных отрезка:
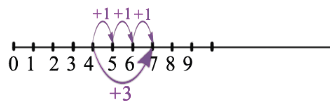
И мы попадем в точку 7, следовательно 4+3=7.
Теперь попробуем отложить на луче, от точки 3 6 единичных отрезков, и от точки 6 3 единичных отрезка, другими словами к 3 прибавим 6 и к 6 прибавим 3 :
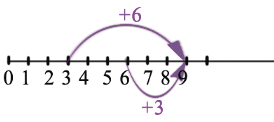
Мы видим, что и в первом и во втором случае мы попадаем в одну и ту же точку: 9, следовательно сумма чисел 3 и 6 и 6 и 3 одинакова и равна 9. Это можно записать с помощью равенства:
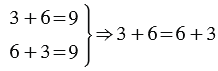
В этом случае мы меняем местами слагаемые и получаем первое свойство сложения - переместительное свойство:
От перестановки слагаемых сумма не меняется
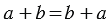
Рассмотрим с помощью координатного луча следующие суммы: 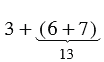 и
и 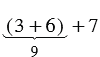 , для этого от точки 3 сначала отложим (6+7) единичных отрезков, а затем от точки 3, отложим сначала 6 единичных отрезков, а затем от получившийся точки отложим еще 7 единичных отрезков:
, для этого от точки 3 сначала отложим (6+7) единичных отрезков, а затем от точки 3, отложим сначала 6 единичных отрезков, а затем от получившийся точки отложим еще 7 единичных отрезков:
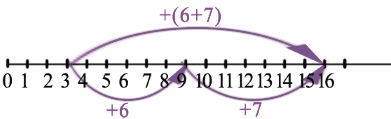
Заметим, что и в первом и во втором случае мы попадаем в одну точку: 16. Это можно записать равенством:
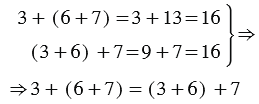
Мы получили второе свойство сложения - сочетательное свойство:
- Чтобы прибавить к числу сумму двух чисел, можно сначала прибавить первое слагаемое, а потом к полученной сумме прибавить второе слагаемое
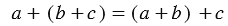
К натуральному числу можно прибавлять не только натуральное число, но еще и нуль, изобразим на луче прибавление нуля к 7:
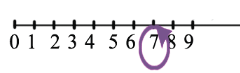
Так как нам необходимо отложить от точки 0 единичных отрезков, то мы попадаем снова в ту же точку,т.е. значение числа от прибавления к нему нуля не изменилось: 7+0=7 . Применив переместительное свойство получим: 7+0=0+7=7, отсюда получаем третье свойство сложения - свойство нуля:
- Если прибавить к нулю какое-нибудь число, то получится прибавленное число
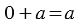
Свойства сложения
- Переместительное свойство
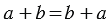
Пример: 9+8=8+9=17
- Сочетательное свойство
Чтобы прибавить к числу сумму двух чисел, можно сначала прибавить первое слагаемое, а потом к полученной сумме прибавить второе слагаемое
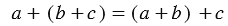
Пример: 7+(3+9)=(7+3)+9=19
- Свойство нуля
Если прибавить к нулю какое-нибудь число, то получится прибавленное число
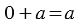
Пример: 0+10=10
Сравнение сумм натуральных чисел
Сравним (15+81) и (15+77), для этого рассмотрим слагаемые этих двух сумм: Мы видим, что первые слагаемые у них одинаковые, поэтому переходим к сравнению вторых слагаемых: 81 >77, поэтому (15+81)>(15+77).
Теперь сравним (21+15) и (34+54), для этого опять рассмотрим слагаемые, в данном случае одинаковых у нас нет, но мы видим, что слагаемые первой суммы меньше слагаемых второй суммы, а значит мы можем записать: (21+15)<(34+54).
Бывают случаи, когда нельзя однозначно сказать, какая сумма больше. Например сравним суммы: (26+33) и (18+43), мы видим, что первое слагаемое первой суммы больше первого слагаемого второй суммы, но второе слагаемое первой суммы меньше второго слагаемого второй суммы. В таком случае необходимо наши суммы привести к виду первого примера, т.е. 26=18+8, следовательно, 26+33=(18+8)+33=18+8+33=18+41, теперь мы сравниваем (18+41) и (18+43), первые слагаемые равны, а 41<43, следовательно(18+41)<(18+43) и мы можем сказать, что (26+33)<(18+43).
Из выше сказанного, делаем вывод: При увеличении слагаемых сумма увеличивается, а при уменьшении уменьшается.
Письменный прием сложения ("сложение в столбик")
Часто при решении задач, нам необходимо складывать многозначные числа, поэтому считать в "уме" или чертить координатный луч не целесообразно, для решения таких задач был придуман письменный прием сложения или "сложение в столбик", который помогает сложение многозначных чисел свести к сложению однозначных чисел, которое мы можем производить легко. Рассмотрим пример:
| 1 | 1 | 1 | |||
| + | 4 | 5 | 8 | 7 | 1 |
| 4 | 3 | 8 | 2 | ||
| 5 | 0 | 2 | 5 | 3 |
Сложение начинаем справа, с разряда единиц: 1+2=3, записываем 3 под единицами, и переходим в разряд десятков: 7+8=15 >10, значит единицы десятков(5) записываем под десятками, а десяток десятков - это единица сотен, записываем ее над разрядом сотен, чтобы не забыть и переходим в следующий разряд: 8+3+1=12 >10, поступаем аналогично, единицы(2) записываем под рассматриваемым разрядом, а десятки записываем над следующим разрядом, далее складываем единицы тысяч: 5+4+1=10=10, здесь 0 единиц, поэтому под рассматриваемым разрядом ставим нуль, а десяток переносим в разряд десятков тысяч: 4+1=5. Получаем, что 45871+4382=50253.
Вывод: Если при сложении чисел одного разряда число получается больше или равное 10, то 1 десяток записываем над следующим разрядом, а единицы под рассматриваемым разрядом.
Советуем посмотреть:
Степень числа. Квадрат и куб числа
Меньше или больше на сколько? во сколько раз?
Представление числовой информации в таблицах
Натуральные числа и действия над ними
Правило встречается в следующих упражнениях:
5 класс
Задание 5.107, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 6.87, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание П.78, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 1.83, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 3.41, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 3.50, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 3.211, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 2, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 5.349, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Номер 254, Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 947, Мерзляк, Полонский, Якир, Учебник
Задание 497, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 581, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 588, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1.20, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 1.47, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 1.144, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 2.94, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 1.46, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 3, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
7 класс
Номер 11, Мерзляк, Полонский, Якир, Учебник
Номер 12, Мерзляк, Полонский, Якир, Учебник
Номер 177, Мерзляк, Полонский, Якир, Учебник
Номер 178, Мерзляк, Полонский, Якир, Учебник
Номер 497, Мерзляк, Полонский, Якир, Учебник
Номер 706, Мерзляк, Полонский, Якир, Учебник
Номер 1006, Мерзляк, Полонский, Якир, Учебник
Упражнение 32, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 55, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 88, Макарычев, Миндюк, Нешков, Суворова, Учебник
8 класс
Номер 67, Мерзляк, Полонский, Якир, Учебник
Номер 578, Мерзляк, Полонский, Якир, Учебник