Окружность, вписанная в правильный многоугольник
Теорема
| В любой правильный многоугольник можно вписать окружность, и притом только одну. |
Доказательство
Дано: А1А2А3...Аn - правильный многоугольник.
Доказать: в многоугольник А1А2А3...Аn можно вписать окружность, и притом только одну.
Доказательство:
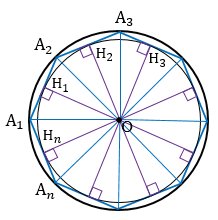
А1А2А3...Аn - правильный многоугольник, значит, мы можем описать около него окружность. Пусть окружность с центром О описана около многоугольника А1А2А3...Аn.
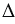 А1ОА2 =
А1ОА2 = 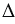 А2ОА3 = ... =
А2ОА3 = ... = 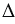 А1ОАn по трем сторонам (ОА1 = ОА2 = ... = ОАn, как радиусы описанной окружности и А1А2 = А2А3 = ... = АnА1, как стороны правильного многоугольника), тогда и высоты этих треугольников, проведенные из вершины О, также будут равны: ОН1 = ОН2 = ... = ОНn. Следовательно, окружность с центром О и радиусом ОН1 проходит через точки Н1, Н2, ..., Нn и касается сторон многоугольника в этих точках, т.е. эта окружность вписана в данный правильный многоугольник А1А2А3...Аn.
А1ОАn по трем сторонам (ОА1 = ОА2 = ... = ОАn, как радиусы описанной окружности и А1А2 = А2А3 = ... = АnА1, как стороны правильного многоугольника), тогда и высоты этих треугольников, проведенные из вершины О, также будут равны: ОН1 = ОН2 = ... = ОНn. Следовательно, окружность с центром О и радиусом ОН1 проходит через точки Н1, Н2, ..., Нn и касается сторон многоугольника в этих точках, т.е. эта окружность вписана в данный правильный многоугольник А1А2А3...Аn.
Докажем, что вписать можно только одну окружность.
Пусть существует окружность с центром О1, вписанная в многоугольник А1А2А3...Аn, отличная от окружности с центром О и радиусом ОН1. Тогда ее центр О1 равноудален от сторон многоугольника, т.е. точка О1 лежит на каждой из биссектрис углов многоугольника А1А2А3...Аn и, следовательно, совпадает с точкой О пересечения этих биссектрис (смотри теорему об окружности, описанной около правильного многоугольника). Радиус этой окружности равен расстоянию от точки О до сторон многоугольника,т.е. равен ОН1. Значит, получаем, что вторая окружность совпадает с первой. Следовательно, наше предположение неверно, и в правильный многоугольник вписать можно только одну окружность. Теорема доказана.
Следствие 1
| Окружность, вписанная в правильный многоугольник, касается сторон многоугольника в их серединах. |
Следствие 2
| Центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в тот же многоугольник. |
Эта точка называется центром правильного многоугольника.
Советуем посмотреть:
Окружность, описанная около правильного многоугольника
Построение правильных многоугольников
Длина окружности и площадь круга
Правило встречается в следующих упражнениях:
7 класс
Задание 1086, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1088, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1130, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1140, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1146, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1281, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1285, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 5, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 6, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 11, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник