Окружность, описанная около правильного многоугольника

Теорема

Доказательство

Дано: А₁А₂А₃...А_n - правильный многоугольник.

Доказать: около А₁А₂А₃...А_n можно описать окружность, и притом только одну.

Доказательство:

Пусть точка О - точка пересечения биссектрис углов А₁ и А₂. Соединим точку О отрезками с остальными вершинами многоугольника и докажем, что ОА₁ = ОА₂ = ... = ОА_n.

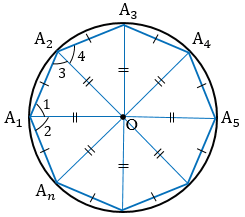
А₁А₂А₃...А_n - правильный многоугольник, значит,  А₁ =  А₂, тогда  1 = 3 (т.к. ОА₁ и ОА₂ биссектрисы равных углов А₁ и А₂), следовательно, $$

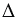А₁ОА₂ - равнобедренный (по признаку равнобедренного треугольника), поэтому ОА₁ = ОА₂.

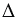А₁ОА₂ = 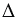А₂ОА₃ по двум сторонам и углу между ними (А₁А₂ = А₂А₃ как стороны правильного многоугольника, ОА₂ - общая, 3 = 4, т.к. ОА₂ биссектриса угла А₂), следовательно,

ОА₁ = ОА₃. Аналогично можно доказать, что ОА₂ = ОА₄, ОА₃ = ОА₅ и т.д.

Итак, ОА₁ = ОА₂ = ... = ОА_n, значит, точка О равноудалена от всех вершин многоугольника. Поэтому окружность с центром О и радиусом ОА₁ является описанной около многоугольника А₁А₂А₃...А_n.

Докажем, что описать можно только одну окружность.

Рассмотрим какие-нибудь три вершины многоугольника А₁А₂А₃...А_n, например, А₁, А₂, А₃. Мы можем начертить только одну окружность одновременно проходящую через три точки А₁, А₂, А₃ (смотри доказательство), т.е. другой окружности проходящей через три данные точки не существует, значит, около многоугольника А₁А₂А₃...А_n можно описать только одну окружность, т.к. точки А₁, А₂, А₃ - вершины данного многоугольника. Теорема доказана.