Длина окружности
Если представить, что окружность сделана из тонкой нерастяжимой нити, которую мы разрежем в произвольной точке А и распрямим её, то длина полученного отрезка АА1 будет являться длиной окружности:

Впишем в окружность равносторонний треугольник, квадрат и правильный двенадцатиугольник:
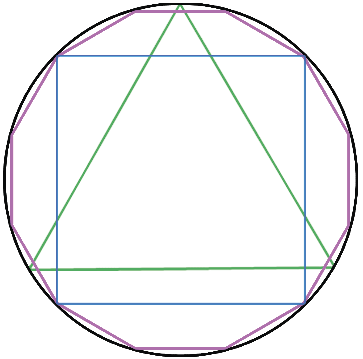
Мы видим, что периметр любого правильного многоугольника, который вписан в окружность является приближённым значением длины окружности, при этом чем больше число сторон такого многоугольника, тем точнее это приближение, так как при неограниченном увеличении количества сторон правильного многоугольника его периметр будет как угодно мало отличаться от длины окружности. Иными словами, предел к которому стремится периметр правильного вписанного в окружность многоугольника при неограниченном увеличении числа его сторон, есть точное значение длины окружности.
Рассмотрим две окружности радиусом 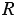 и
и 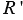 . Обозначим длину этих окружностей через
. Обозначим длину этих окружностей через 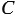 и
и 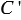 соответственно. Впишем в каждую из них
соответственно. Впишем в каждую из них 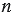 - угольник. Пусть
- угольник. Пусть 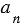 и
и 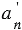 - стороны данных многоугольников, а
- стороны данных многоугольников, а 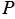 и
и 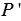 - их периметры:
- их периметры:
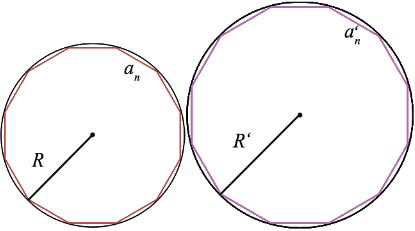
Периметры данных многоугольников вычисляют по формулам:
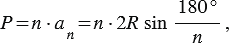
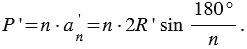
Поделим первое равенство на второе и получим, что:
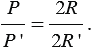 (1)
(1)
Это равенство справедливо для любого значения 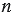 . Если мы будем неограниченно увеличивать число
. Если мы будем неограниченно увеличивать число 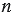 , то периметры
, то периметры 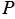 и
и 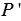 соответственно будут сколь угодно мало отличаться от длин
соответственно будут сколь угодно мало отличаться от длин 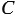 и
и 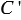 описанных окружностей. Значит, при неограниченном увеличении
описанных окружностей. Значит, при неограниченном увеличении 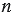 отношение
отношение 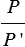 будет сколь угодно мало отличаться от отношения
будет сколь угодно мало отличаться от отношения 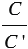 . Учитывая равенство (1), получаем, что число
. Учитывая равенство (1), получаем, что число 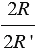 сколь угодно мало отличается от числа
сколь угодно мало отличается от числа 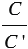 , значит,
, значит, 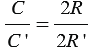 или
или 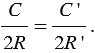
Из последнего равенства очевидно, что для всех окружностей отношение длины окружности к диаметру есть одно и то же число. Данное число принято обозначать греческой буквой 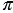 (читается "пи"), т.е.
(читается "пи"), т.е. 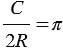 , отсюда получаем, что длину окружности можно найти по формуле:
, отсюда получаем, что длину окружности можно найти по формуле: 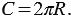
Число 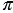 иррациональное, а значит, оно не может быть представлено в виде конечной десятичной дроби. При решении задач в качестве приближённого значения
иррациональное, а значит, оно не может быть представлено в виде конечной десятичной дроби. При решении задач в качестве приближённого значения 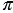 принимают число
принимают число 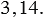
Очевидно, что длина 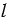 дуги окружности с градусной мерой
дуги окружности с градусной мерой 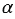 выражается формулой
выражается формулой 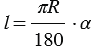 , так как длина всей окружности равна
, так как длина всей окружности равна 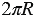 . Таким образом, длина дуги в 10 равна
. Таким образом, длина дуги в 10 равна 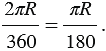
Советуем посмотреть:
Окружность, описанная около правильного многоугольника
Окружность, вписанная в правильный многоугольник
Построение правильных многоугольников
Длина окружности и площадь круга
Правило встречается в следующих упражнениях:
7 класс
Задание 1101, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1105, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1109, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1140, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1142, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1216, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 9, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 10, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 11, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 17, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник