Радианная мера угла
Длина дуги выражается формулой: 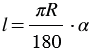 .
.
Если 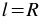 , то
, то 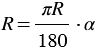 , откуда
, откуда 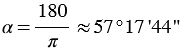 .
.
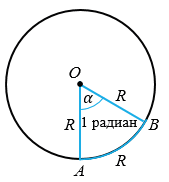
Градусная мера дуги, которую мы получили, меньше 1800, значит, соответствующий дуге центральный угол окружности имеет такую же градусную меру. Причем, найденное значение 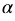 не зависит от выбора окружности, поэтому такой центральный угол часто выбирается за единицу измерения углов, и называется углом в 1 радиан или радианом.
не зависит от выбора окружности, поэтому такой центральный угол часто выбирается за единицу измерения углов, и называется углом в 1 радиан или радианом.
Получается, градусная мера угла в 1 радиан составляет 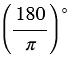 .
.
Радианная мера угла - положительное число 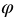 , которое показывает, сколько раз радиан и его части укладываются в некотором угле.
, которое показывает, сколько раз радиан и его части укладываются в некотором угле.
Определим, какова связь между градусной и радианной мерой одного и того же угла. Из определения радиана следует, что углу, градусная мера которого равна 1800, соответствует 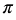 радиан.Тогда углу в 10 соответствует в 180 раз меньше, т.е.
радиан.Тогда углу в 10 соответствует в 180 раз меньше, т.е. 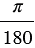 радиан. Получается, углу, градусная мера которого равна
радиан. Получается, углу, градусная мера которого равна 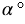 , соответствует
, соответствует 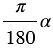 радиан. Если
радиан. Если 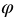 - радианная мера угла, то ей соответствует градусная мера
- радианная мера угла, то ей соответствует градусная мера 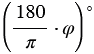 .
.
Градусная мера угла не превосходит 1800, поэтому и радианная мера угла не превосходит 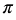 радиан.
радиан.
Если дуга окружности меньше полуокружности или равна полуокружности, то ее радианная мера также не превосходит 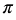 радиан. Если дуга окружности больше полуокружности, то ее радианная мера больше
радиан. Если дуга окружности больше полуокружности, то ее радианная мера больше 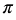 радиан.
радиан.
Формула, для вычисления длины 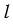 дуги окружности радиуса
дуги окружности радиуса 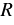 через ее радианную меру
через ее радианную меру 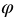 , имеет следующий вид:
, имеет следующий вид: 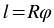 .
.
Доказательство:
Радианной мере 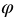 соответствует градусная мера
соответствует градусная мера 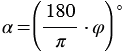 , при этом
, при этом 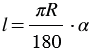 , тогда
, тогда 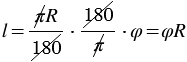 .
.
Советуем посмотреть:
Окружность, описанная около правильного многоугольника
Окружность, вписанная в правильный многоугольник
Построение правильных многоугольников
Длина окружности и площадь круга
Правило встречается в следующих упражнениях:
7 класс
Задание 1203, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1204, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1220, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 11, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 12, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 13, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник