Построение правильных многоугольников
Задача 1
Построить правильный шестиугольник, сторона которого равна данному отрезку.
Дано: отрезок DC.
Построить: правильный шестиугольник, сторона которого равна DC.
Решение:

Для решения задачи воспользуемся тем, что сторона шестиугольника равна радиусу описанной около него окружности, т.е. 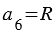 (смотри формулу для вычисления стороны правильного многоугольника), где
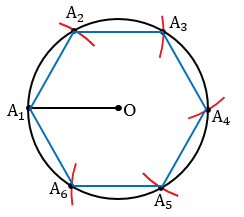
(смотри формулу для вычисления стороны правильного многоугольника), где 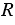 - радиус окружности описанной около правильного многоугольника. Нам нужно построить правильный шестиугольник со стороной DC, поэтому с помощью циркуля измеряем отрезок DC и строим окружность радиуса DC, и отмечаем на ней произвольную точку А1, центр окружности обозначаем буквой О.
- радиус окружности описанной около правильного многоугольника. Нам нужно построить правильный шестиугольник со стороной DC, поэтому с помощью циркуля измеряем отрезок DC и строим окружность радиуса DC, и отмечаем на ней произвольную точку А1, центр окружности обозначаем буквой О.
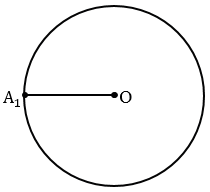
Затем не меняя раствора циркуля, построим на этой окружности точки А2, А3, А4, А5, А6, так, чтобы выполнялись равенства
А1А2 = А2А3 = А3А4 = А4А5 = А5А6 = DC (т.е. сначала строим окружность радиуса DC с центром в точке А1 (всю окружность строить необязательно, смотри выделенное красным), данная окружность пересечет окружность с центром О в точке А2, далее аналогично строим окружность радиуса DC с центром в точке А2, она пересечет окружность с центром О в точке А3 и т.д.).
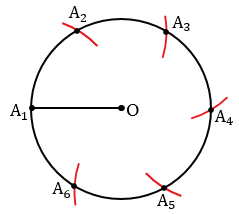
Теперь соединяя последовательно построенные точки отрезками, получим искомый правильный шестиугольник А1А2А3А4А5А6.
Задача 2
Дан правильный 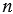 -угольник. Построить правильный 2
-угольник. Построить правильный 2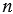 -угольник.
-угольник.
Дано: правильный 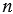 -угольник А1А2А3...Аn.
-угольник А1А2А3...Аn.
Построить: правильный 2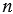 -угольник.
-угольник.
Решение:
Пусть, например, нам дан шестиугольник А1А2А3А4А5А6, значит, построить нужно двенадцатиугольник.
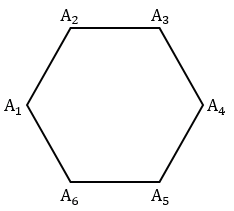
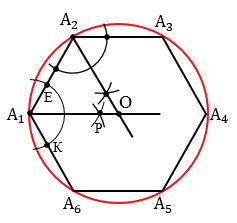
Сначала опишем около данного шестиугольника А1А2А3А4А5А6 окружность. Для этого построим биссектрисы углов А1 и А2. Чтобы построить биссектрису угла А1, строим окружность произвольного радиуса с центром в точке А1 (полностью окружность строить необязательно, смотри выделенное красным цветом), данная окружность пересечет стороны А1А2 и А1А6 угла А1 в точках Е и К. Затем строим две окружности с центрами в точках Е и К радиуса ЕК (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом), данные окружности пересекутся в точке Р. Далее проводим луч А1Р, который и будет биссектрисой угла А1.
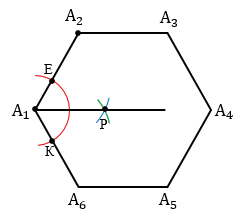
Аналогично строим биссектрису угла А2.
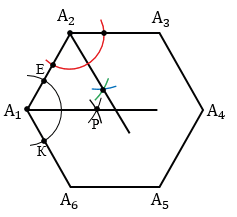
Точку пересечения биссектрис углов А1 и А2 обозначаем буквой О и строим окружность радиуса ОА1 с центром О (окружность описанная около А1А2А3А4А5А6).
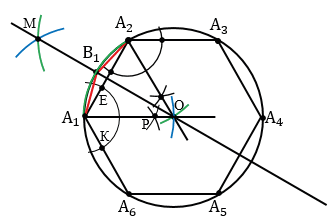
Далее нужно каждую из дуг А1А2, А2А3, А3А4, А4А5, А5А6, А6А1 разделить пополам. Чтобы разделить дугу А1А2 пополам, построим серединный перпендикуляр к отрезку А1А2. Для этого строим две окружности с центрами в точках А1 и А2 радиуса А1А2 (полностью окружность строить необязательно, смотри выделенное красным цветом). Данные окружности пересекутся в двух точках, одну обозначим буквой М, а другая совпадет с точкой О, т.к. у шестиугольника сторона равна радиусу (с другими многоугольниками совпадения с точкой О не будет) . Затем проводим прямую МО, данная прямая пересечет дугу А1А2 в точке В1, которая и разделит дугу А1А2 пополам. Далее точку В1 соединяем с концами А1 и А2 дуги А1А2.
Аналогично находим точки В2, В3. Точки В4, В5, В6 в данном случае строить необязательно, они получаются автоматически при построении точек В1, В2, В3, т.к. шестиугольник симметричная фигура.
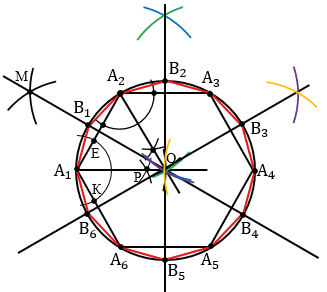
Получили двенадцатиугольник А1В1А2В2А3В3А4В4А5В5А6В6 (смотри выделенное красным).
Мы выполняли построения на примере правильного шестиугольника, если мы имеем произвольный правильный 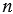 -угольник, то все построения выполняются аналогично.
-угольник, то все построения выполняются аналогично.
Применяя указанный способ, можно с помощью циркуля и линейки построить целый ряд правильных многоугольников, если построен один из них. Например, построив правильный треугольник и пользуясь результатом задачи 2, можно построить правильный шестиугольник, затем правильный двенадцатиугольник и вообще 2k-угольник, где 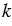 - любое целое число, больше двух.
- любое целое число, больше двух.
Замечание
Не все правильные многоугольники можно построить с помощью циркуля и линейки. Доказано, например, что правильный семиугольник не может быть построен при помощи циркуля и линейки.
Советуем посмотреть:
Окружность, описанная около правильного многоугольника
Окружность, вписанная в правильный многоугольник
Длина окружности и площадь круга
Правило встречается в следующих упражнениях:
7 класс
Задание 1100, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник