Аксиома параллельных прямых
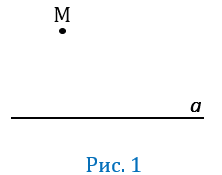
Рассмотрим произвольную прямую  и точку М, не лежащую на ней (Рис.1).
и точку М, не лежащую на ней (Рис.1).
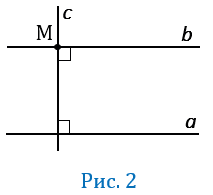
Докажем, что через точку М можно провести прямую, параллельную прямой  . Для этого проведем через точку М две прямые: сначала прямую
. Для этого проведем через точку М две прямые: сначала прямую 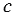 перпендикулярно к прямой
перпендикулярно к прямой  , а затем прямую
, а затем прямую  перпендикулярно к прямой
перпендикулярно к прямой 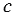 (Рис.2). А из того, что две прямые
(Рис.2). А из того, что две прямые  и
и  перпендикулярны к третьей прямой
перпендикулярны к третьей прямой 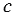 следует, что они параллельны (
следует, что они параллельны (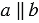 ).
).
Возникает вопрос: можно ли через точку М провести еще одну прямую, параллельную прямой  ?
?
Если прямую  "повернуть" на какой-то угол вокруг точки М, то она пересечет прямую
"повернуть" на какой-то угол вокруг точки М, то она пересечет прямую  (прямая
(прямая  ' на рис.3).
' на рис.3).
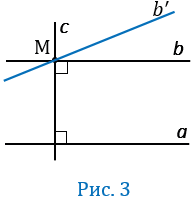
То есть нам кажется, что через точку М нельзя провести прямую отличную от прямой  , параллельную прямой
, параллельную прямой  . Утверждение о единственности прямой, проходящей через данную точку параллельно данной прямой, не может быть доказано на основе остальных аксиом Евклида, а само является аксиомой.
. Утверждение о единственности прямой, проходящей через данную точку параллельно данной прямой, не может быть доказано на основе остальных аксиом Евклида, а само является аксиомой.
Аксиома параллельных прямых
| Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной. |
Следствия из аксиомы параллельных прямых
| 10. Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую. |
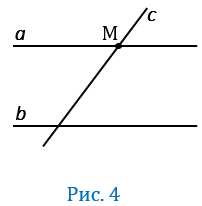
Дано: 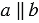 ,
, 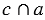 = М (Рис.4).
= М (Рис.4).
Доказать: 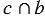 .
.
Доказательство:
Если мы предположим, что прямая 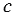 не пересекает прямую
не пересекает прямую  , то прямая
, то прямая 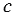 будет параллельна прямой
будет параллельна прямой  , а по условию через точку М проходит прямая
, а по условию через точку М проходит прямая  параллельная прямой
параллельная прямой  , значит получим, что через точку М будут проходить две прямые
, значит получим, что через точку М будут проходить две прямые  и
и 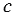 параллельные прямой
параллельные прямой  (Рис.5).
(Рис.5).
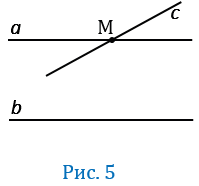
Но это противоречит аксиоме параллельных прямых, значит, наше предположение неверно, и прямая 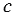 пересекает прямую
пересекает прямую  , т.е.
, т.е. 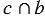 . Что и требовалось доказать.
. Что и требовалось доказать.
| 20. Если две прямые параллельны третьей прямой, то они параллельны. |
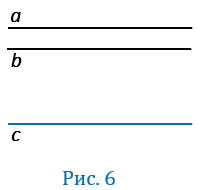
Дано: 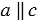 ,
, 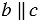 (Рис.6).
(Рис.6).
Доказать: 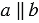 .
.
Доказательство:
Предположим, что прямые  и
и  не параллельны, т.е. пересекаются в некоторой точке М (Рис.7).
не параллельны, т.е. пересекаются в некоторой точке М (Рис.7).
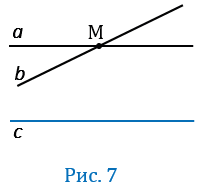
Тогда получим, что через точку М проходят две прямые  и
и  параллельные прямой
параллельные прямой 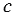 , т.к. по условию
, т.к. по условию 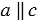 и
и 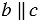 . Но это противоречит аксиоме параллельных прямых, следовательно, наше предположение неверно, значит, прямые
. Но это противоречит аксиоме параллельных прямых, следовательно, наше предположение неверно, значит, прямые  и
и  параллельны, т.е.
параллельны, т.е. 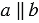 . Что и требовалось доказать.
. Что и требовалось доказать.
Следствие - утверждение, которое выводится непосредственно из аксиом или теорем.
Советуем посмотреть:
Признаки параллельности двух прямых
Практические способы построения параллельных прямых
Теорема о накрест лежащих углах
Теорема о соответственных углах
Теорема об односторонних углах
Теорема об углах с соответственно параллельными сторонами
Теорема об углах с соответственно перпендикулярными сторонами
Правило встречается в следующих упражнениях:
7 класс
Задание 196, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 198, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 199, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 213, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 282, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 567, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 568, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 645, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 9, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 13, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник