Задание 453 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№453 учебника 2013-2022 (стр. 122):
Как изменится площадь прямоугольника, если: а) одну пару противоположных сторон увеличить в два раза; б) каждую сторону увеличить в два раза; одну пару противоположных сторон увеличить в два раза, а другую - уменьшить в два раза?
№453 учебника 2023-2024 (стр. 120):
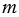 является касательной к каждой из них в точках А и В соответственно. Докажите, что отрезок АВ равен отрезку О1О2.
является касательной к каждой из них в точках А и В соответственно. Докажите, что отрезок АВ равен отрезку О1О2.Подсказка
№453 учебника 2013-2022 (стр. 122):
Вспомните:
- Какой четырехугольник называется прямоугольником.
- Как найти площадь прямоугольника.
№453 учебника 2023-2024 (стр. 120):
Вспомните:
- Что называют окружностью.
- Что называют отрезком.
- Какую прямую называют касательной к окружности, ее свойства.
- Параллельные прямые.
- Расстояние между параллельными прямыми.
- Какой треугольник называют прямоугольным.
- Признаки равенства прямоугольных треугольников.
- Какие фигуры называют симметричными относительно прямой.
- Какие углы называют вертикальными, их свойство.
Ответ
№453 учебника 2013-2022 (стр. 122):




№453 учебника 2023-2024 (стр. 120):
Дано: окр.(О1, r), окр.(О2, r), M - их точка касания, 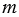 - касательная, А и В точки касания.
- касательная, А и В точки касания.
Доказать: АВ = О1О2.
Доказательство:
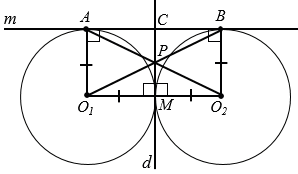
1. Пусть d - общая касательная данных окружностей, т.е. М 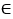 d,
d, 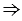 О1М
О1М 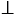 d и О2М
d и О2М 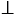 d.
d.
2. В прямоугольных 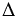 О1РМ и
О1РМ и 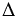 О2РМ:
О2РМ:
О1М = О2М = r и РМ - общая, 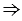
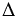 О1РМ =
О1РМ = 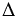 О2РМ по двум катетам,
О2РМ по двум катетам, 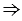
О1Р = О2Р.
3. 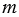 - касательная, А и В точки касания,
- касательная, А и В точки касания, 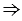 О1А
О1А 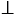
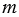 и О2В
и О2В 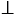
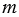 ,
, 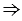 О1А
О1А 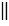 О2В и
О2В и 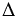 О1АВ и
О1АВ и 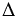 О2ВА - прямоугольные, и в них: О1А = О2В = r и АВ - общая,
О2ВА - прямоугольные, и в них: О1А = О2В = r и АВ - общая, 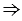
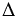 О1АВ =
О1АВ = 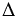 О2ВА по двум катетам,
О2ВА по двум катетам, 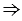 АО2 = ВО1, при этом О1Р = О2Р,
АО2 = ВО1, при этом О1Р = О2Р, 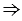 АР = ВР.
АР = ВР.
4. АО2 = ВО1, О1Р = О2Р и АР = ВР, при этом Р 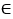 d,
d, 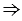 d - ось симметрии отрезков АО2 и ВО1,
d - ось симметрии отрезков АО2 и ВО1, 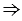 АС = ВС, при этом О1М = О2М и О1А
АС = ВС, при этом О1М = О2М и О1А 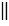 О2В,
О2В, 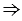
АВ = О1О2.
Что и требовалось доказать.
Пояснения:
Чтобы выполнить доказательство делаем дополнительное построение: проводим общую касательную d для двух окружностей через точку М. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания, тогда О1М 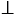 d и О2М
d и О2М 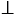 d, следовательно,
d, следовательно, 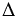 О1РМ и
О1РМ и 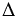 О2РМ - прямоугольные. При этом в них:
О2РМ - прямоугольные. При этом в них:
О1М = О2М = r (по условию окружности одинакового радиуса) и РМ - общая, значит, 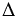 О1РМ =
О1РМ = 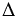 О2РМ по двум катетам. В равных треугольниках против равных углов лежат равные стороны, поэтому О1Р = О2Р.
О2РМ по двум катетам. В равных треугольниках против равных углов лежат равные стороны, поэтому О1Р = О2Р.
По условию прямая 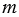 является касательной к каждой из данных окружностей в точках А и В соответственно, значит, О1А
является касательной к каждой из данных окружностей в точках А и В соответственно, значит, О1А 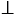
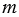 и О2В
и О2В 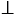
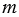 , тогда О1А
, тогда О1А 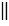 О2В, т.к. две прямые перпендикулярные к третьей прямой параллельны. Также
О2В, т.к. две прямые перпендикулярные к третьей прямой параллельны. Также 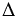 О1АВ и
О1АВ и 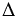 О2ВА - прямоугольные, и в них:
О2ВА - прямоугольные, и в них:
О1А = О2В = r и АВ - общая, следовательно, 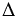 О1АВ =
О1АВ = 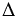 О2ВА по двум катетам, тогда АО2 = ВО1, при этом О1Р = О2Р, тогда и АР = ВР.
О2ВА по двум катетам, тогда АО2 = ВО1, при этом О1Р = О2Р, тогда и АР = ВР.
Итак, АО2 = ВО1, О1Р = О2Р и АР = ВР и Р 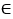 d, значит, d - ось симметрии отрезков АО2 и ВО1, тогда АС = ВС, при этом О1М = О2М и О1А
d, значит, d - ось симметрии отрезков АО2 и ВО1, тогда АС = ВС, при этом О1М = О2М и О1А 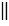 О2В, следовательно, АВ = О1О2, т.к. все точки каждой из двух параллельных прямых равноудалены от другой прямой. Что и требовалось доказать.
О2В, следовательно, АВ = О1О2, т.к. все точки каждой из двух параллельных прямых равноудалены от другой прямой. Что и требовалось доказать.
Вернуться к содержанию учебника