Упражнение 723 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 194

\[40\text{ мин}=\frac{40}{60}\text{ ч}=\frac{2}{3}\text{ ч}\]

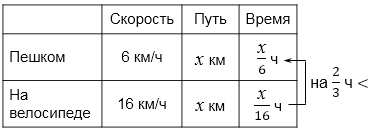
Составим уравнение:

\(\frac{x}{6}-\frac{x}{16}=\frac{2}{3}\)  \(/\times 48\)

\(8x - 3x = 32\)

\(5x = 32\)

\(x = \frac{32}{5}\)

\(x = 6,4\)

Ответ: 6,4 км от фермы до станции.

Пояснения:

Основная формула движения:

\[t=\frac{s}{v}\]

где \(t\) — время,

\(s\) — расстояние,

\(v\) — скорость.

Так как расстояние одинаковое, обозначаем его через \(x\).

Время в пути пешком:

\[t_1=\frac{x}{6}\]

Время в пути на велосипеде:

\[t_2=\frac{x}{16}\]

По условию на велосипеде Пётр тратит на \(40\) минут меньше. Сначала переводим минуты в часы:

\[40\text{ мин}=\frac{2}{3}\text{ часа}\]

Разность времени равна \(\frac{2}{3}\) часа:

\[\frac{x}{6}-\frac{x}{16}=\frac{2}{3}\]

Умножаем обе части уравнения на общий знаменатель \(48\):

\[\frac{16x-6x}{96}=\frac{10x}{96}\]

Выполнив преобразования получаем линейное уравнение:

\(5x=32\), откуда \(x=6{,}4\).

Значит, расстояние от фермы до станции равно \(6,4\) км.