Упражнение 724 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 194

\[4\text{ ч }30\text{ мин}=4{,}5\text{ ч}\]

\[30\text{ мин}=0{,}5\text{ ч}\]

\(4,5 - 0,5 = 4\) (ч) - время в пути из-за задержки.

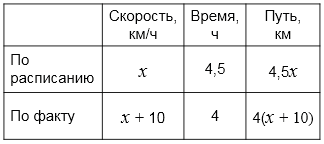
Составим уравнение:

\(4,5x = 4(x+10)\)

\[4{,}5x=4x+40\]

\[4{,}5x-4x=40\]

\[0{,}5x=40\]

\(x = \frac{40}{0,5}\)

\(x = \frac{400}{5}\)

\[x=80\]

\(80\) км/ч - скорость поезда по расписанию.

\(4{,}5\cdot 80=360\) (км)

Ответ: \(360\) км между городами А и В.

Пояснения:

Основная формула движения:

\[s = vt\]

где \(t\) — время,

\(s\) — расстояние,

\(v\) — скорость.

По расписанию поезд должен пройти путь за \(4\) ч \(30\) мин, что равно \(4{,}5\) часа.

Так как отправление задержали на \(30\) минут (\(0{,}5\) часа), фактически на движение осталось \(4{,}5-0{,}5=4\) часа.

Обозначим скорость по расписанию через \(x\) км/ч, а время в пути по расписанию \(4,к\) ч, тогда расстояние между городами А и В будет равно \(4,5x\) км.

После увеличения, скорость станет равной \(x + 10\) км/ч, а время движения \(4\) ч, тогда расстояние между городами А и В равно \(4(x + 10)\) км.

Приравнивая выражения для расстояния между городами А и В, получаем уравнение:

\(4,5x = 4(x+10)\),

откуда, выполнив преобразования получаем \(x = 80\).

Значит, скорость движения поезда по расписанию составляет \(80\) км/ч.

Подставляя значение скорости в выражение для расстояния \(4,5x\), находим расстояние между городами А и В - \(360\) км.